人员安排问题--搜索算法的剪支方法应用

问题定义

       输入：

• 人的集合P = {P₁,P₂,...,P_n}，其中，P₁<P₂<...<P_n
•  工作的集合J = {J₁,J₂,...,J_n}，J是偏序集合，也就是说，J中某些元素之间存在序关系
• 矩阵[C_ij]，C_ij表示工作J_j分配给P_i的代价

       输出：

• 每个人都被分配到某一工作，不同人分配到不同工作，且满足以下条件：如果F(Pi) ≤ F(Pj)，那么Pi<Pj。其中，F:P→J,表示p被分配给工作j。
• 矩阵[Xij]，Xij = 1表示Jj分配给Pi，Σ
  

分析以及生成解空间

      定义1：J的拓扑序列<J_K1,J_K2,...J_Kn>。满足，如果 J_i ≤ J_j，那么J_i排在J_j。

      命题1：如果P₁→J_k1,P₂→J_k2,..,P_n→J_kn是一个可能 解, 当且仅当J_k1,J_k2,...,J_kn必是一个J的拓朴排序的序列。

      证明1：显然，依据问题的定义可以直接证明得到。

      拓扑排序树问题

      输入：偏序集合J

      输出：J的拓扑序列树，即用树表示所有的拓扑排序序列<J_K1,J_K2,...J_Kn>。满足，如果 J_i ≤ J_j，那么J_i排在J_j。

输入: 偏序集合S, 树根root.
输出: 由S的所有拓朴排序序列构成的树.
生成树根root;
选择偏序集中没有前序元素的所有元素, 作为root的子节点;
For root的每个字节点v Do
     S=S-{v};
把v作为根, 递归地处理S

      拓扑序列树的例子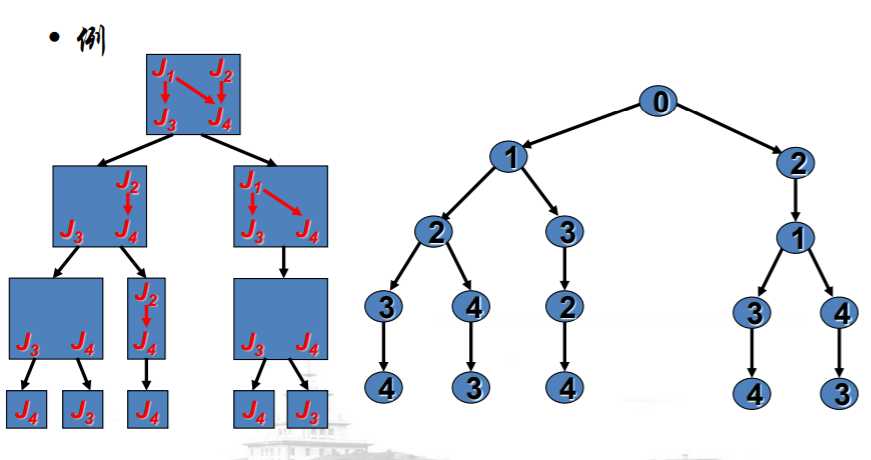

分支界限搜索方法

        该问题变为对拓扑序列树的最大权值序列的搜索问题。

        命题2，把代价矩阵某行(列)的各元素减去同一个 数, 不影响优化解的求解，同时，所有被减去元素的和 + 某一序列对于当前权值矩阵计算的和 =  该序列对于原权值矩阵计算的和，且将所有被减去元素的和定义为解的代价下界。

        证明2，该序列仅仅在权值矩阵的每一行(列)选取一个元素，也必会选取一个元素，那么，把代价矩阵某行(列)的各元素减去同一个数，并不会影响对于该行(列)元素的选取。

        技巧1，代价矩阵的每行(列)减去同一个数(该行或列的最小数), 使得每行和每列至少有一个零, 其余各元素非负。

       搜索算法可以定义为：

• 建立根节点,，其权值为解代价下界：技巧1中所有被减去元素的和;
• 使用爬山法, 求解出当前算法的某个代价较小的可行解， 计算代价方法为：每产生一个节点,，其权值为加工后的代价矩阵对应元素加其父节点权值;
• 当发现某个可行解时，遍历所有的解，在这一过程中，不断较低界限以及根据界限删去不可能是优化解的部分(剪支)。

人员安排问题--搜索算法的剪支方法应用

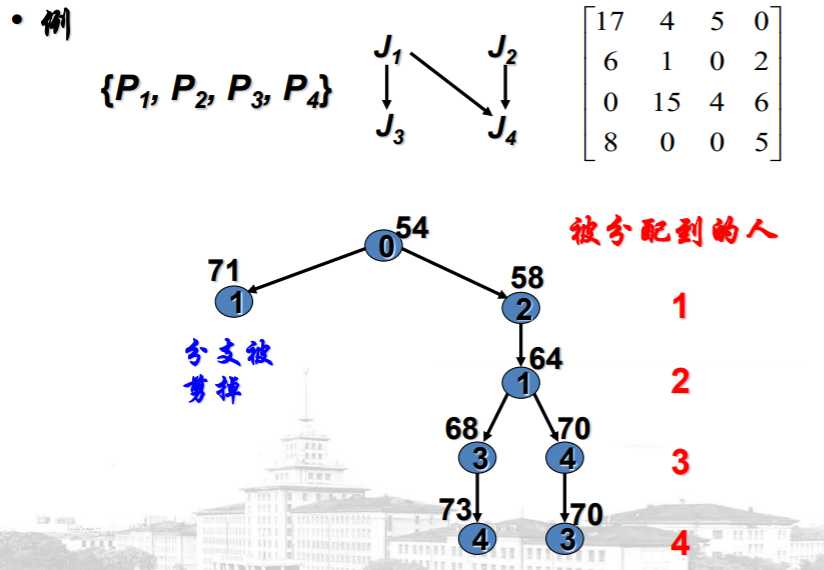
原文：https://www.cnblogs.com/zqybegin/p/13598677.html