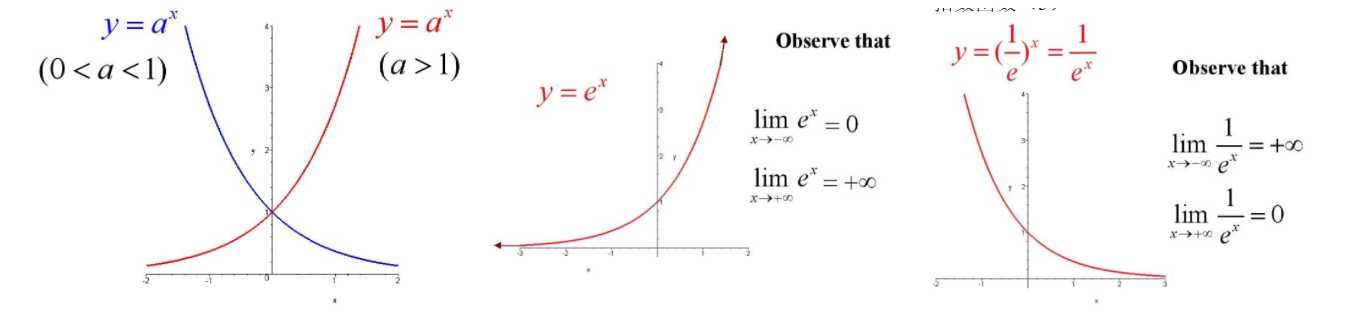
自然常数 e = 2.71828183,是一个无限不循环小数。
圆周率 pi = 3.1415926
假设A是条件,B是结论
(1)由A可以推出B,由B可以推出A,则A是B的充要条件(A=B)
(2)由A可以推出B,由B不可以推出A,则A是B的充分不必要条件(A?B)
(3)由A不可以推出B,由B可以推出A,则A是B的必要不充分条件(B?A)
(4)由A不可以推出B,由B不可以推出A,则A是B的既不充分也不必要条件(A¢B且B¢A)
1.两数绝对值之差的绝对值小于等于两数之差的绝对值
2.一个正数加它的倒数恒大于等于2
3.基本不等式:两个正实数的算术平均数大于或等于它们的几何平均数。
(a-b)^2 = a^2 - 2ab + b^2
则 2ab < a^2 + b^2,两个或者三个数相乘时就要想到他。
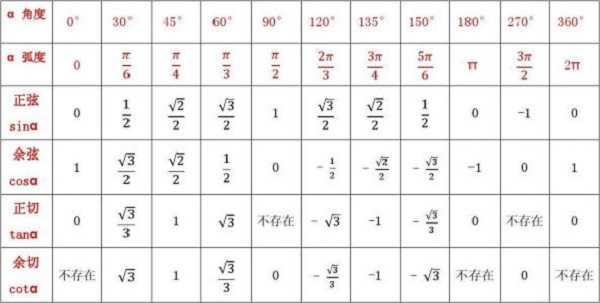
4.sin x与x与tan x之间的关系
5.x与ln(1+x)之间的关系
完全平方:(a+b)^2 = a^2 + 2ab + b^2
平方和:1^2 + 2^2 + 3^2 + …… + n^2 = n(n+1)(2n+1)/6
平方差:a^2 - b^2 = (a+b)(a-b)
立方和:a^3 + b^3 = (a+b)(a^2+ab+b^2)
立方差:a^3 - b^3 = (a-b)(a^2+ab+b^2)
一个常用的变形:
另一个常用变形:
除此之外做题碰到的一个
对数可以让乘除变加减
【定义】如果\(N=a^x(a;0,a≠1)\),即a的x次方等于N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作:\(x=log_aN\)
其中,a叫做对数的底数,N叫做真数,x叫做“以a为底N的对数”。
对数的一些基本性质:


排列,就是指从给定个数的元素中取出指定个数的元素进行排序。
组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
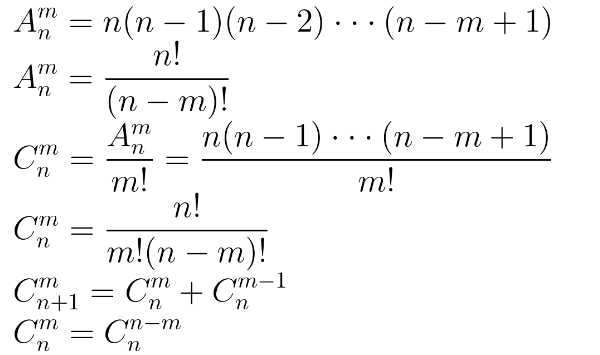



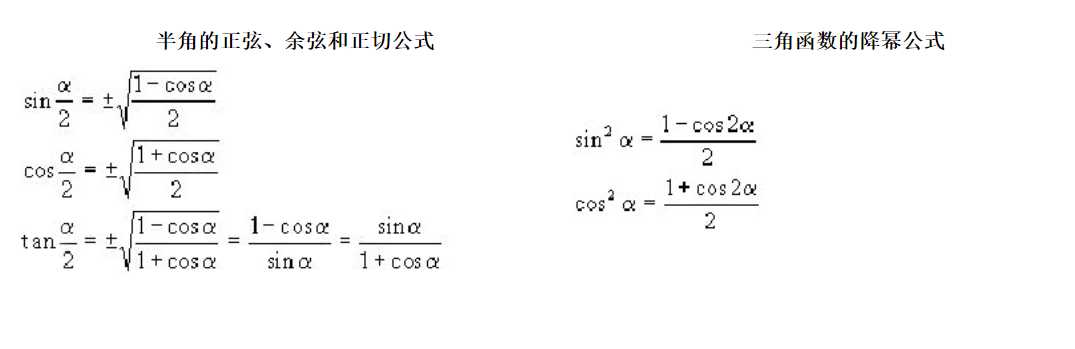



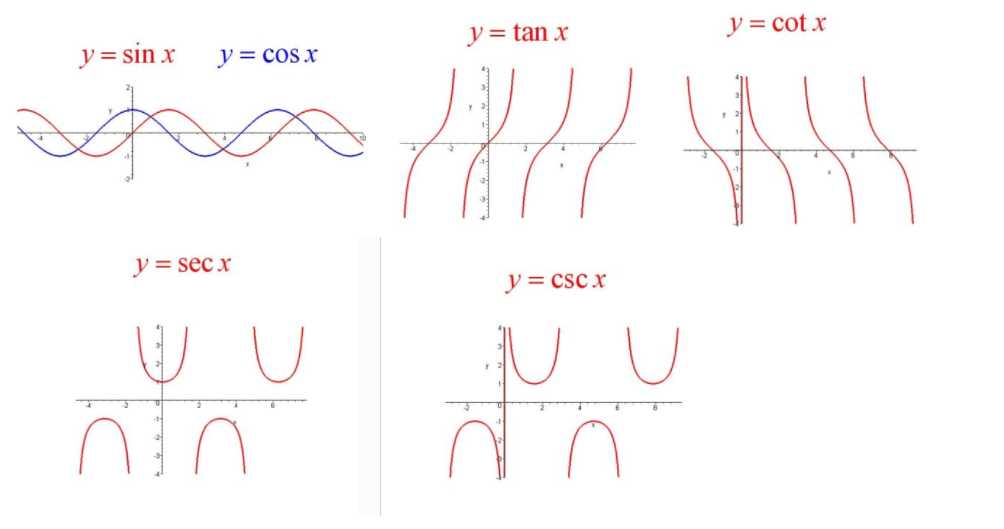
sec x是正割,$ \sec x = \frac{1}{\cos x} $
csc x是余割,\(\csc x = \frac{1}{\sin x}\)
cot x是余切,\(\cot x = \frac{\cos x}{\sin x}\)
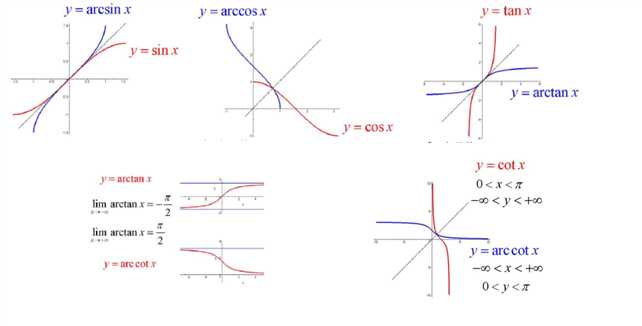
y=arcsin(x),定义域[-1,1],值域[-π/2,π/2]
y=arccos(x),定义域[-1,1],值域[0,π]
y=arctan(x),定义域(-∞,+∞),值域(-π/2,π/2)
y=arccot(x),定义域(-∞,+∞),值域(0,π)
sin(arcsinx)=x,定义域[-1,1],值域[-1,1]arcsin(-x)=-arcsinx
正弦定理: R为三角形外接圆的半径
余弦定理:
参考链接:https://wenku.baidu.com/view/d66747d176eeaeaad1f33099.html
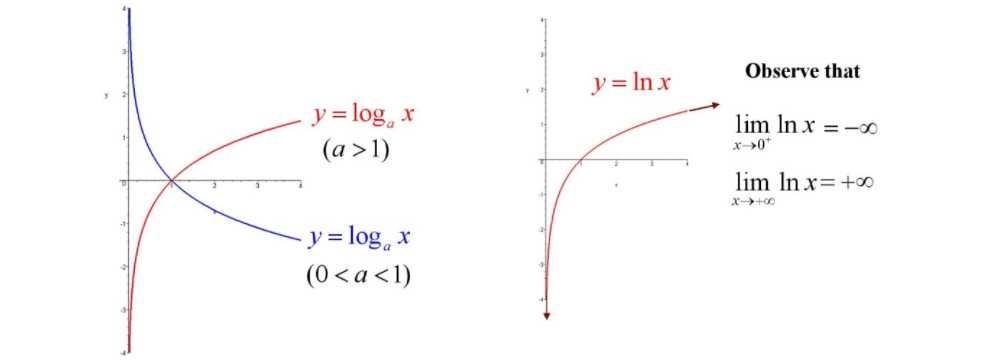
空间直角坐标系
过空间定点O作三条互相垂直的数轴,它们都以O为原点,具有相同的单位长度.这三条数轴分别称为X轴(横轴).Y轴(纵轴).Z轴(竖轴),统称为坐标轴。
各轴之间的顺序要求符合右手法则,即以右手握住Z轴,让右手的四指从X轴的正向以90度的直角转向Y轴的正向,这时大拇指所指的方向就是Z轴的正向。这样的三个坐标轴构成的坐标系称为右手空间直角坐标系.与之相对应的是左手空间直角坐标系.一般在数学中更常用右手空间直角坐标系,在其他学科方面因应用方便而异。
三条坐标轴中的任意两条都可以确定一个平面,称为坐标面.它们是:由X轴及Y轴所确定的XOY平面;由Y轴及Z轴所确定的YOZ平面;由X轴及Z轴所确定的XOZ平面.这三个相互垂直的坐标面把空间分成八个部分,每一部分称为一个卦限.位于X,Y,Z轴的正半轴的卦限称为第一卦限,从第一卦限开始,在XOY平面上方的卦限,按逆时针方向依次称为第二,三,四卦限;第一,二,三,四卦限下方的卦限依次称为第五,六,七,八卦限。
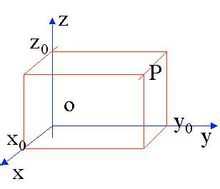
右手坐标系
要标注X、Y和Z轴的正轴方向,就将右手背对着屏幕放置,拇指即指向X轴的正方向。伸出食指和中指,如下图所示,食指指向Y轴的正方向,中指所指示的方向即是Z轴的正方向。要确定轴的正旋转方向,如下图所示,用右手的大拇指指向轴的正方向,弯曲手指。那么手指所指示的方向即是轴的正旋转方向。

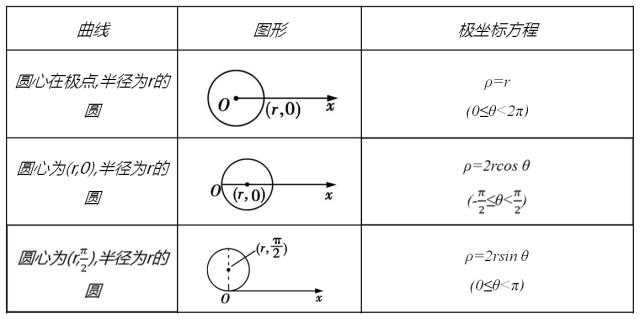
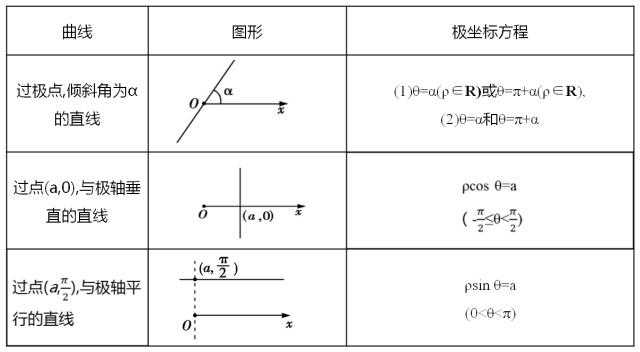
极坐标系
极坐标系是一个二维坐标系,该坐标系统中任意位置可由一个夹角和一段相对原点——极点的距离来表示。
极坐标系是指在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点O,称为极点。从O出发引一条射线Ox,称为极轴。再取定一个单位长度,通常规定角度取逆时针方向为正。这样,平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定,有序数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ);ρ称为P点的极径,θ称为P点的极角。
常见的极坐标方程
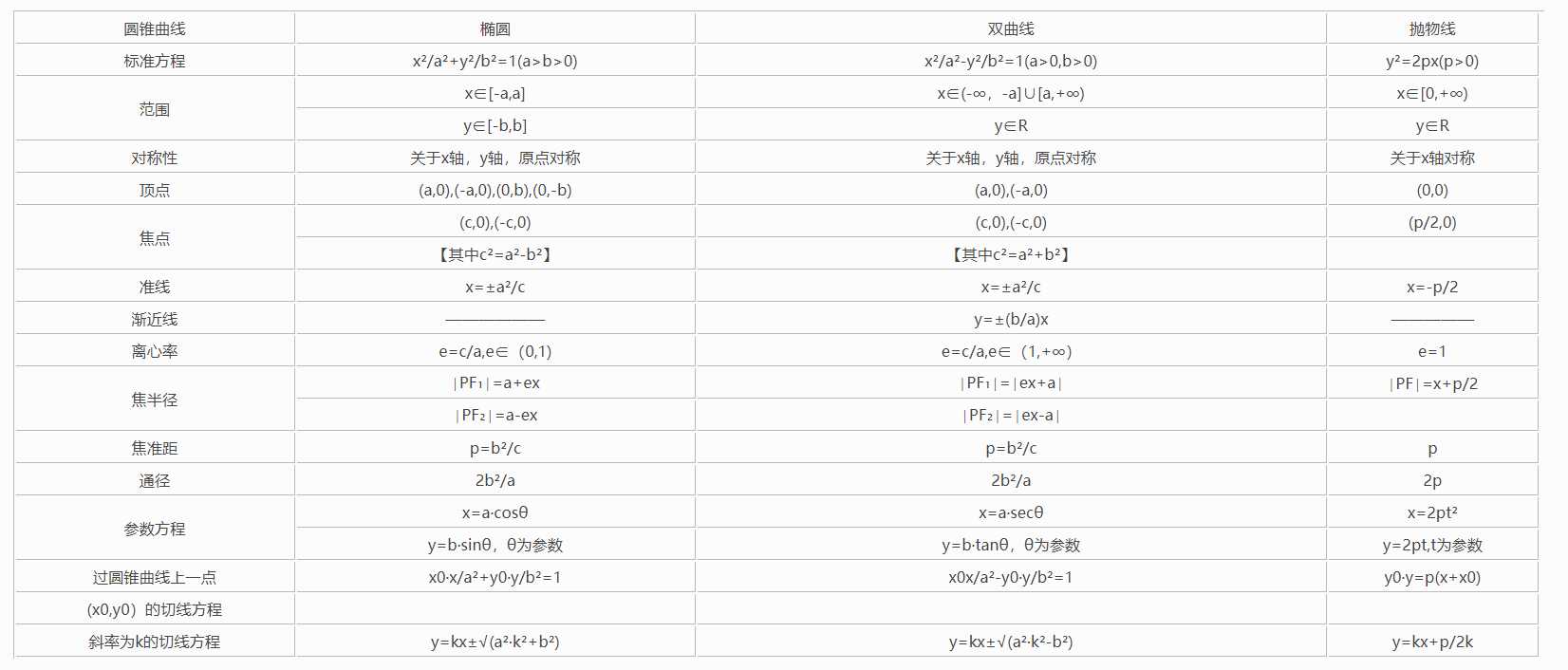
圆锥曲线的统一定义:到定点的距离与到定直线的距离的商是常数e的点的轨迹。
椭圆:
1、中心在原点,焦点在x轴上的椭圆标准方程:其中x2/a2+y2/b2=1,其中a>b>0,c2=a2-b2
2、中心在原点,焦点在y轴上的椭圆标准方程:y2/a2+x2/b2=1,其中a>b>0,c2=a2-b2
参数方程:x=acosθ;y=bsinθ(θ为参数,0≤θ≤2π)
椭圆面积公式:s=πab
双曲线:
1、中心在原点,焦点在x轴上的双曲线标准方程:x2/a-y2/b2=1,其中a>0,b>0,c2=a2+b2.
2、中心在原点,焦点在y轴上的双曲线标准方程:y2/a2-x2/b2=1,其中a>0,b>0,c2=a2+b2.
参数方程:x=asecθ;y=btanθ(θ为参数)
抛物线:
参数方程:x=2pt2;y=2pt(t为参数)t=1/tanθ(tanθ为曲线上点与坐标原点确定直线的斜率)特别地,t可等于0
直角坐标:y=ax2+bx+c(开口方向为y轴,a≠0)x=ay2+by+c(开口方向为x轴,a≠0)
两条直线垂直,其斜率乘积为-1.
点斜式:\(y - y_0 = k(x - x_0)\)
斜截式:\(y = kx + b\) ,与y轴交点为(0,b)
两点式:\(\frac{y - y_1}{y - y_2} = \frac{x - x_1}{x - x_2}\) 。过两点。
截距式:\(\frac{x}{a} + \frac{y}{b} = 1\) ,x截距为a,y截距为b。
一般式:\(Ax + By + C = 0\)
两点之间的距离公式:\(d = \sqrt{(x_2-x_1)^2 + (y_2 - y_1)^2}\)
点到直线的距离公式:\(d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}\)
两条平行直线的距离公式:\(d = \frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}\)
圆的一般方程为\(x2+y2+Dx+Ey+F=0(D2+E2-4F > 0)\),或可以表示为\((X+D/2)2+(Y+E/2)2=(D2+E2-4F)/4\)。
标准方程:\((x-a)^2 + (y-b)^2 = R^2\)。圆心为(a,b),半径为R。
球:\(V = \frac{4}{3}\pi R^3\).
圆锥:\(V =\frac{1}{3}\pi R^2h\).
原文:https://www.cnblogs.com/colourso/p/12976891.html