二叉树可以用于排序。其原理很简单:对于一个排序二叉树添加新节点时,先与根节点比较,若小则交给左子树继续处理,否则交给右子树。
当遇到空子树时,则把该节点放入那个位置。
比如,10 8 5 7 12 4 的输入顺序,应该建成二叉树如下图所示,其中.表示空白。
...|-12 10-| ...|-8-| .......|...|-7 .......|-5-| ...........|-4
本题目要求:根据已知的数字,建立排序二叉树,并在标准输出中横向打印该二叉树。
输入数据为一行空格分开的N个整数。 N<100,每个数字不超过10000。
输入数据中没有重复的数字。
输出该排序二叉树的横向表示。为了便于评卷程序比对空格的数目,请把空格用句点代替:
...|-20 10-| ...|-5
.......|-20 ..|-10-| ..|....|-8-| ..|........|-7 5-| ..|-4
这题初看,除了知道这些数值是自顶向下递减的,其他没什么头绪,然后看了网上的一些代码,但是本人的代码阅读能力有些差,还是实力太差了,所以愣是看不大懂,不过总算也提取了些重要的信息.
1.声明一个变量用于存储根节点的值;
2.开辟两个数组L[]和R[]分别用于存储每个节点的左子树和右子树的信息;
3.写一个add()函数处理添加新节点的操作.
了解了这些之后我就开始自己在纸上写写画画,既然知道了节点的行号,那么也要确定其列号才行,然后发现除了根节点列号为0,每个节点的列号正好是其父节点的列号+父节点的数值长度+3(这个3即"-|-"的长度),于是我开辟了一个数组pos[]用于记录节点的列号,数组len[]记录数字长度. 于是写出如下(有bug的)代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <string> 6 #include <cmath> 7 #include <algorithm> 8 #define INF 0x3f3f3f3f 9 #define zero 1e-7 10 11 using namespace std; 12 typedef long long ll; 13 const ll mod=1e9+7; 14 const ll max_n=105; 15 16 int a[max_n]={0};//记录输入的数字 17 int L[max_n]={0};//记录节点的左子树 18 int R[max_n]={0};//记录节点的右子树 19 int pos[max_n]={0};//记录节点的列号 20 int len[max_n]={0};//记录数字的长度 21 22 //添加新节点 23 void add(int r, int x) { 24 if(x<r) {//若x<r则将x交给r的左子树处理 25 if(!L[r]) {//若r的左子树为空,则将x放入这个位置 26 L[r]=x; 27 pos[x]=pos[r]+len[r]+3;//x的列号,3是"-|-"的长度 28 } 29 else { 30 add(L[r], x); 31 } 32 } 33 else {//否则将x交给r的左子树处理 34 if(!R[r]) { 35 R[r]=x; 36 pos[x]=pos[r]+len[r]+3; 37 } 38 else { 39 add(R[r], x); 40 } 41 } 42 } 43 44 int main() { 45 int k=0;//k记录输入数字的个数 46 int root;//记录根节点的值 47 while(cin>>a[k]) { 48 int temp=a[k]; 49 while(temp) {//计算数字a[k]的长度 50 len[a[k]]++; 51 temp/=10; 52 } 53 if(!k) {//第一个输入的数字是根节点 54 root=a[k]; 55 pos[a[k]]=0; 56 } 57 else { 58 add(root, a[k]); 59 } 60 k++; 61 } 62 sort(a, a+k, greater<int>());//按降序排列,由排序二叉树的特性可知,自顶往下数值越小 63 for(int i=0; i<k; i++) {//打印输出 64 for(int j=0; j<pos[a[i]]-2; j++) { 65 cout<<‘.‘; 66 } 67 if(a[i]!=root) cout<<"|-"; 68 cout<<a[i]; 69 if(L[a[i]] || R[a[i]]) cout<<"-|"; 70 cout<<endl; 71 } 72 return 0; 73 }
运行之后输出是这样的(Ctrl+Z+回车 结束输入得结果)——
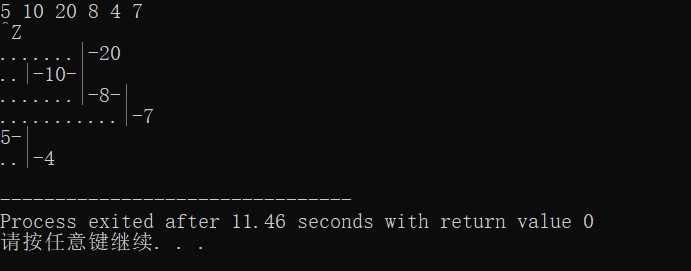
没错,漏了好几个‘|‘,因为我只在节点前面添加了‘|‘,而忽略了每个父节点从其右子树到左子树的纵向之间的‘|‘,这可如何是好,想了想,于是我开辟了一个二维数组mp[][]用于记录数字前面的‘.‘,‘|‘ 和‘-‘,并写了两个循环,一个用于填满每行数字前面的‘.‘,‘|‘和‘-‘,一个用于专门处理每个父节点从其右子树到左子树的纵向之间的‘|‘,也就是64~89行的代码,当然打印输出那里也改了一下,以下是修改后的AC代码——
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <string> 6 #include <cmath> 7 #include <algorithm> 8 #define INF 0x3f3f3f3f 9 #define zero 1e-7 10 11 using namespace std; 12 typedef long long ll; 13 const ll mod=1e9+7; 14 const ll max_n=105; 15 16 char mp[max_n][max_n];//记录数字前面的‘.‘,‘|‘ 和‘-‘ 17 int a[max_n]={0};//记录输入的数字 18 int L[max_n]={0};//记录节点的左子树 19 int R[max_n]={0};//记录节点的右子树 20 int pos[max_n]={0};//记录节点的列号 21 int len[max_n]={0};//记录数字的长度 22 23 //添加新节点 24 void add(int r, int x) { 25 if(x<r) {//若x<r则将x交给r的左子树处理 26 if(!L[r]) {//若r的左子树为空,则将x放入这个位置 27 L[r]=x; 28 pos[x]=pos[r]+len[r]+3;//x的列号,3是"-|-"的长度 29 } 30 else { 31 add(L[r], x); 32 } 33 } 34 else {//否则将x交给r的左子树处理 35 if(!R[r]) { 36 R[r]=x; 37 pos[x]=pos[r]+len[r]+3; 38 } 39 else { 40 add(R[r], x); 41 } 42 } 43 } 44 45 int main() { 46 int k=0;//k记录输入数字的个数 47 int root;//记录根节点的值 48 while(cin>>a[k]) { 49 int temp=a[k]; 50 while(temp) {//计算数字a[k]的长度 51 len[a[k]]++; 52 temp/=10; 53 } 54 if(!k) {//第一个输入的数字是根节点 55 root=a[k]; 56 pos[a[k]]=0; 57 } 58 else { 59 add(root, a[k]); 60 } 61 k++; 62 } 63 sort(a, a+k, greater<int>());//按降序排列,由排序二叉树的特性可知,自顶往下数值越小 64 //这个循环是将每行的数字前面填满‘.‘,‘|‘和‘-‘ 65 for(int i=0; i<k; i++) { 66 int j; 67 for(j=0; j<pos[a[i]]-2; j++) { 68 mp[i][j]=‘.‘; 69 } 70 mp[i][j++]=‘|‘; 71 mp[i][j]=‘-‘; 72 } 73 //这个循环是处理每个节点从其右子树到左子树的纵向之间的‘|‘ 74 for(int i=0; i<k; i++) { 75 int temp=pos[a[i]]+len[a[i]]+1;//这是节点a[k]右边的‘|‘的列号 76 if(R[a[i]]) {//若该节点有右子树 77 for(int j=i-1; ; j--) {//往上 78 if(a[j]>=R[a[i]]) break; 79 mp[j][temp]=‘|‘; 80 } 81 } 82 if(L[a[i]]) {//若该节点有左子树 83 for(int j=i+1; ; j++) {//往下 84 if(a[j]<=L[a[i]]) break; 85 mp[j][temp]=‘|‘; 86 } 87 } 88 } 89 for(int i=0; i<k; i++) {//打印输出 90 for(int j=0; j<pos[a[i]]; j++) 91 cout<<mp[i][j]; 92 cout<<a[i]; 93 if(L[a[i]] || R[a[i]]) cout<<"-|"; 94 cout<<endl; 95 } 96 return 0; 97 }
原文:https://www.cnblogs.com/wwqzbl/p/13578271.html