E.Divide Square(树状数组/线段树)(扫描线)

题意:这里有一个\(10^6 \times 10^6\)的平面.你的任务是画一些线段在平面上,所有的线段都是水平的或者垂直的,至少有一侧是挨着平面的边线的.你的任务是数出有多少片被这些线段划分出来.

分析: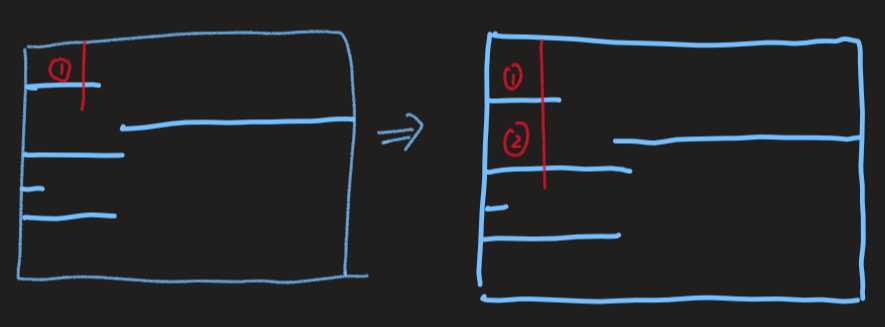,我们先把所有水平的线画出来,可以看到当红线继续穿过一根水平线的时候,平面数会增加一个.当然除了这种情况,如果不考虑相交产生的平面数,那么一根左端点是0,右端点是\(10^6\)的竖线也会增加一个平面.那么就只会有这两种情况会增加平面数.

我们可以枚举每根竖线,然后统计每根竖线和所有水平线的相交数,就是平面的增加数.这个我们可以使用扫描线,考虑一个水平线,它的左端点是它开始出现的点,右端点是它消失的点,我们可以使用树状数组维护,1表示增加,-1表示减少,一根扫描线的属性是[x, y, 1或者-1],一根水平线可以拆分成[x1, y, 1]和[x2, y + 1, -1],我们只要修改在树状数组上的y点即可,然后每次枚举一根竖线,我们把这根竖线x点之前的扫描线都读进来,然后查看在y1, y2之间的点数,即是相交的顶点数.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 1e6 + 5;
struct Seg
{
    int y, x;
    int k;
    bool operator<(const Seg& rhs)const
    {
        return x < rhs.x;
    }
}seg[2 * N];

struct V
{
    int x, y1, y2;
    bool operator<(const V& rhs)
    {
        return x < rhs.x;
    }
}vline[N];

ll c[N];

int lowbit(int x)
{
    return x & (-x);
}

void modify(int x, int d)
{
    for (int i = x; i < N; i += lowbit(i)) c[i] += d;
}

int query(int x)
{
    ll res = 0;
    for (int i = x; i; i -= lowbit(i)) res += c[i];
    return res;
}

int main() {
   
    const int q = 1e6;
    //水平,横
    int n, m;
    scanf("%d%d", &n, &m);

    ll res = 0;
    int num = 0;
    int y, x1, x2;
    for (int i = 1; i <= n; ++i)
    {
        scanf("%d%d%d", &y, &x1, &x2);
        if (x1 == 0 && x2 == q) ++res;
        seg[++num] = { y, x1, 1 };
        seg[++num] = { y, x2 + 1, -1 };
    }

    for (int i = 1; i <= m; ++i)
    {
        scanf("%d%d%d", &vline[i].x, &vline[i].y1, &vline[i].y2);
        if ((vline[i].y1 == 0) && (vline[i].y2 == q)) ++res;
    }

    sort(seg + 1, seg + num + 1);
    sort(vline + 1, vline + m + 1);

    for (int j = 0, i = 1; i <= m; ++i)
    {
        while (j < 2 * n && seg[j + 1].x <= vline[i].x)
        {
            ++j;
            modify(seg[j].y + 1, seg[j].k);
        }
        res += query(vline[i].y2 + 1) - query(vline[i].y1);
    }

    printf("%lld\n", res + 1);

    return 0;
}

E.Divide Square(树状数组/线段树)(扫描线)

原文：https://www.cnblogs.com/pixel-Teee/p/13566215.html