归并排序的核心思想是使用分治的策略来进行排序。分治是将大问题分成一些小问题,小问题解决后在合并在一起。
我们来看一下这一排数据:9,4,5,1,2,7,3,8,6,0。算法流程大概就是以下图所示,将数组拆分,然后每一个小数组进行排序合并。
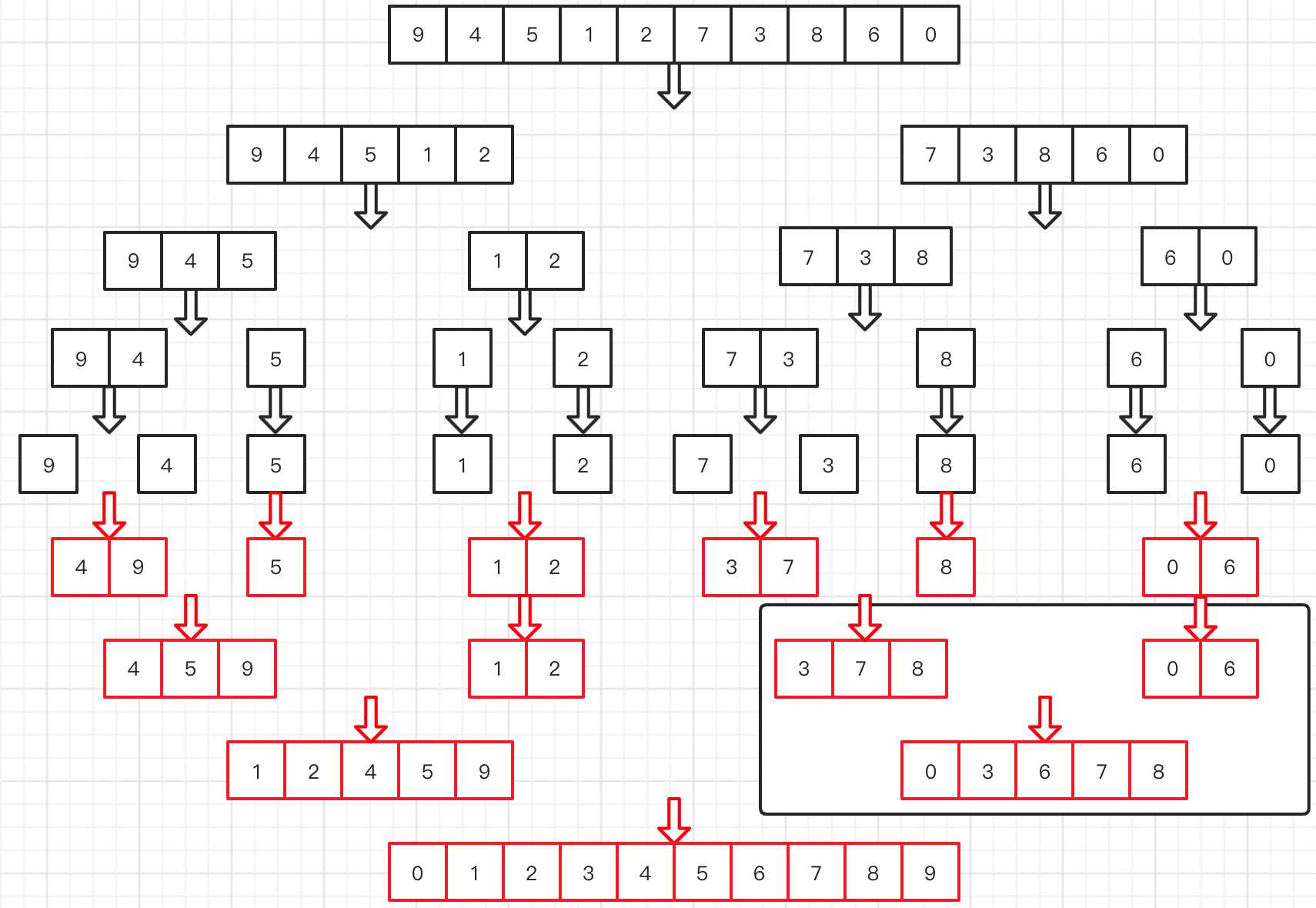
再看一下局部的两个小数组如何进行合并的,进行合并的两个红色数组里面的数已经是有序的,上图黑色框部分
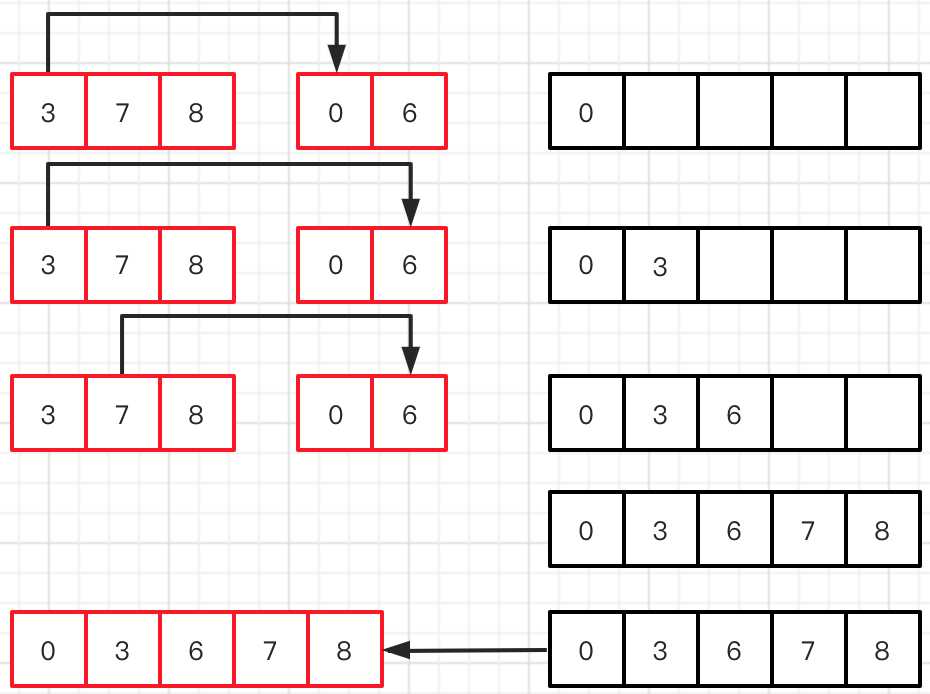
申请一个临时数据,存放排序后的结果。
第一行:红色左边数组跟红色右边数组进行对比,小的就放入黑色的临时数组中
第二行:进行下一个数的对比,将小的放入黑色的临时数组中
第三行:再次进行下一个数的对比
红色右边数组已经对比完,将红色左边数组剩下的数按顺序放入到临时数组中
最后将黑色临时数组的数值拷贝回红色数组。
实现代码:
1 void sortmerge(int *pArray, int nLeft, int nRight) { 2 if(nLeft == nRight) return ; 3 int mid = (nLeft + nRight) / 2; 4 //拆分 5 sortmerge(pArray, nLeft, mid); 6 sortmerge(pArray, mid+1, nRight); 7 //排序合并 8 int x = nLeft; 9 mid = (nLeft + nRight) / 2; 10 int y = mid + 1; 11 int tmpArray[1000]; 12 int ans = 0; 13 while(x <= mid && y <= nRight) { //数组合并进行对比 14 if(pArray[x] < pArray[y]) { 15 tmpArray[ans++] = pArray[x++]; 16 } 17 else { 18 tmpArray[ans++] = pArray[y++]; 19 } 20 } 21 while(x <= mid) { //左边数组还有剩下的数,存入临时数组 22 tmpArray[ans++] = pArray[x++]; 23 } 24 while(y <= nRight) { //右边数组还有剩下的数,存入临时数组 25 tmpArray[ans++] = pArray[y++]; 26 } 27 ans = 0; 28 for(int i=nLeft; i<=nRight; i++) { //将临时数组的数拷贝回原数组中 29 pArray[i] = tmpArray[ans++]; 30 } 31 }

可关注公众号了解更多的面试技巧
原文:https://www.cnblogs.com/yew0/p/13531509.html