在人工智能领域,时序决策是考虑了世界是动态变化的算法,可以认为是一种循序渐进的决策理论,较早的决策会影响较晚的可用选择。例如我们考虑一个推箱子到指定区域的问题,从初始状态(start state)到目标状态(goal state)的一系列动作(action)都会影响到达目标状态的,我们可以把这一过程扩展到策略的概念,即在某个时隙(time slot)中应该做何种动作,这样这一策略的概念为:基于决策理论对于待优化的目标函数最优值(optimality)的计算,策略将所有的状态映射到一个最优的动作。
在上述时序决策提出的问题中,马尔科夫决策过程就是一种正式的框架。在这个模型中,环境通过一组状态和动作进行建模,可以用来执行以控制系统的状态。通过这种方式来控制系统以最大化模型的性能指标。这里说明在这个模型中的基本定义:
Random Variable:随机变量是概率论的基础,可以认为该变量是动态随机变化的,在强化学习中,两个随机变量是相互独立的。举例来说“海水是咸的”是随机变量\(X\)的值,“井水是甜的”是随机变量\(Y\)的值,两者显然相互独立。
Stochastic Process:举例来说,在股市当中,\(t\)时刻股票价格\(S_t\),\(S_t\)是随着时间\(t\)动态变化的,在这一过程中\(S_1\)、\(S_2\)、\(S_3\)、\(S_4\)、……、\(S_t\)变化十分复杂,是一种随机过程,可表示为\(\sum_{i=1}^t{S_t}\)。
Markov Chain:马尔科夫链和马尔科夫过程(Markov Process)指的是同一种东西。即当前时刻的状态仅和上一状态有关,公式表示为:$$P[S_{t+1}|S_t]=P[S_{t+1}|S_1,\cdots,S_t]$$马尔科夫链示意图如下:

State Space Model:状态空间模型可以认为是马尔科夫链加上一个观察值,即表示为\(Markov Chain+Observation\)。包括HMM,Kalman Filter,Particle Filter模型。之所以有观测独立假设,是因为此模型中引入了隐变量。而某时刻观测变量只和此时刻隐变量之间有关系。
Markov Reward Process:马尔科夫回报即:\(Markov Chain+Reward\)。在转移到下一个状态时,会得到一个回报,可通过该回报来评价状态转移。
Markov Decison Process:马尔科夫决策过程即:\(Markov Chain+Reward+Action\)在当前状态可选择一类动作执行,然后通过Reward来评价决策是否合理。马尔科夫链可用下图表示:

MDP可由一个四元数组\(\{\mathcal{S},\mathcal{A},\mathcal{T},\mathcal{R}\}\)表示。
状态\(\mathcal{S}\):当状态空间的规模为N,环境集合S可以定义为有限集合\(\{s^1,\cdots,s^N\}\),即\(|S|=N\)。
动作\(\mathcal{A}\):动作集合mathcal{A}通过有限集合\(\{a^1,\cdots,a^N\}\)来定义。其中,动作空间的大小为K,即\(|A|=K\)。动作可以用于控制系统的状态,能够用于某一特定状态\(s\in{S}\)的动作集合表示为\(A(s)\),其中\(A(s)\subseteq{A}\)。
转换函数\(\mathcal{T}\):通过将动作\(a\in{A}\)应用于状态\(s\in{S}\),基于可能的转换集合的概率分布,学习系统能够完成从当前状态s到新状态\(s‘\in{S}\)的转换。
回报方程\(\mathcal{R}\):回报方程指在一个状态中的奖励,或在一个状态中完成一个动作后的奖励。
转换矩阵也就是转换函数,即转换集合的概率分布。假设系统一共有N状态,表示为\(\mathcal{S}=\{s_1,s_2,\cdots,s_t,\cdots,s_N\}\),那么从\(s_1\)转换到\(s_2\)的概率可表示为\(T(s_1,s_2)\),即转换矩阵可表示为:
考虑动作\(\mathcal{A}\)和回报\(\mathcal{R}\)一个转换概率可表示为:$$P=(s‘,r|s,a) \buildrel\Delta\over= P_r[S_{t+1}=s‘,R_{t+1}=r|S_t=s,A_t=a]$$动态特性由以上这个概率函数可以表现。需要注意的是回报r是一个随机变量,因此状态转移函数并不等于转换概率。因此,状态转移函数与转换概率关系为:
\begin{equation}
T(s,a,s‘)=P(s‘|s,a)=\sum_{r\in{R}}{P(s‘,r|s,a)}\tag{2}
\end{equation}其中\(0 \le T(s,a,s‘) \le 1\),并且\(\sum T(s,a,s‘)=1\)。
什么是策略?在给定的一个马尔科夫决策过程\(<\mathcal{S},\mathcal{A},\mathcal{T},\mathcal{R}>\)中,我们有状态集合\(\mathcal{S}\)以及行为集合\(\mathcal{A}\),那么在给定的一个状态\(s\)中我们要做何种行为\(a\)就叫策略,即表示为:\(\pi:\mathcal{S}\longrightarrow\mathcal{A}\)。策略分两种:
确定性策略:在确定了状态后,只执行特定的动作。注意这个状态跟时间没有关系。比如在状态\(s\)我们只执行动作\(a\),表示为:\(a\buildrel\Delta\over= \pi(s)\)。
随机性策略:在确定了状态后,有多种动作可供选择,并且每种动作按照一定概率分布。表示为:\(\pi(a|s) \buildrel\Delta\over= P_r\{A_t=a|S_t=s\}\)。
如何衡量一个策略的好坏呢?我们在状态\(S_t\)做出动作\(A_t\),只要使得获得的回报函数\(R_{t+1}=r\)最大就行。然而这只考虑到下一个状态回报,并没有考虑到全局,这种方法称为贪心算法。
我们知道,评价策略的好坏就是通过回报(奖励函数)来评判。事实上,马尔科夫决策过程学习的目标就是收集回报,尽可能的让回报最大。一个简单的最优准则就是优化回报\(G_t=R_{t+1}+R_{t+2}+\cdots+R_{T}\),如果我们考虑长期回报,但是根据接收时间的远近将在未来受到打折。打个比方讲,张三伤害了李四,李四在第一天是十分痛苦的,但是久而久之这种痛苦可能会逐渐减弱。因此这里引入阻尼系数\(\gamma\),\(0\le \gamma <1\)。这样回报表示为:
\begin{equation}
G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots+\gamma^{h-1} R_{t+h}=\sum_{i=0}\gamma^i{R_{t+i+1},\quad r\in[0,1)}\tag{3}
\end{equation}然而,回报只能对应马尔科夫决策过程中的其中一条路径。系统根据不同的动作及回报会有多种状态转移路径,如图所示:
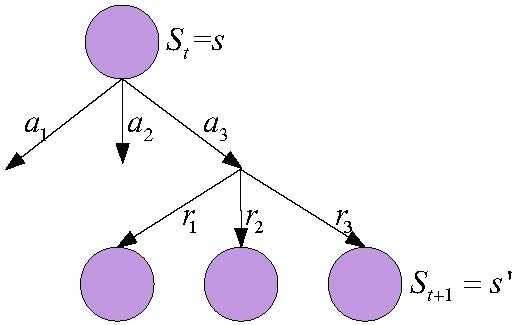
根据上图,我们知道,此图例中可以看到一共有9种转移可能,可以记为\(G_t^1\)、\(G_t^2\)、\(\cdots\)、\(G_t^9\),并不是单独的一个\(G_t\)。所以,我们就可以用这个9个可能的平均值来表示最终的衡量标准。而实际中由于可能性很多,通常通过蒙特卡罗采样来求平均值得到最终的函数值,也就是价值函数:
\begin{equation}
V^{\pi}(s)=\mathbb{E}_\pi [G_t|S_t=s]\tag{4}
\end{equation}
价值函数可以分为两种:
状态价值函数:
有一个自变量。
状态—动作价值函数:
这里引入了动作,指在某种状态下确定一个动作。状态价值函数和动作价值函数关系可表示为:
\begin{equation}
\begin{split}
V^{\pi}(s)&=\pi(a_1|s)Q^\pi(s,a_1)+\pi(a_2|s)Q^\pi(s,a_2)+\pi(a_3|s)Q^\pi(s,a_3)+\cdots \
&=\sum\limits_{a\in \mathcal{A}(s)}^\infty \pi(a|s) Q_{\pi}(s,a)
\end{split}\tag{7}
\end{equation}通过式子\((7)\)我们知道\(V^{\pi}(s)\)是\(Q_{\pi}(s,a)\)的加权平均值,对式子\((5)\)展开:
\begin{equation}
\begin{split}
Q^{\pi}(s,a) &= \sum_{r,s‘}P(s‘,r|s,a)[\sum\limits_{k = 0}^\infty\gamma^kR^{t+k}|S_t=s] \
&= \sum_{r,s‘}P(s‘,r|s,a)[R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\cdots|S_t=s] \
&= \sum_{r,s‘}P(s‘,r|s,a)[r+\gamma V^\pi (s‘)]
\end{split}\tag{8}
\end{equation}将式\((8)\)代入式\((7)\)得到状态价值的贝尔曼期望方程:
\begin{equation}
V^{\pi}(s) = \sum\limits_{a\in \mathcal{A}(s)}^\infty \pi(a|s)\sum_{r,s‘}P(s‘,r|s,a){r+\gamma V^\pi (s‘)}\tag{9}
\end{equation}将式\((7)\)代入式\((8)\)得到状态-动作的贝尔曼期望方程:
\begin{equation}
Q^{\pi}(s,a) = \sum_{r,s‘}P(s‘,r|s,a){r+\gamma \sum\limits_{a‘\in \mathcal{A}(s‘)}^\infty \pi(a‘|s‘) Q_{\pi}(s‘,a‘)}\tag{10}
\end{equation}
式\((9)\)、式\((10)\)为贝尔曼期望方程。对于式\((9)\),\(V_\pi\)是这组方程的唯一解,对于多个策略可以有相同的价值功能,但对于给定的策略\(\pi\),\(V_\pi\)是独一无二的。对于任何给定的马尔科夫决策过程的目标是找到一个最优策略,即获得最多的回报(奖励)策略。这意味着对所有状态\(s \in \mathcal{S}\)最大化式\((5)\)。最优策略表示为\(\pi ^*\),设定:
这个表达式称为贝尔曼最优方程,一个最优策略下的状态值必须等于在该状态下的最优行为回报。为了选择了最优状态的价值函数\(V_*\)的最优行为,可以有以下规则:
\begin{equation}
\pi ^*(s) = \arg\max_\pi V_\pi(s) = \arg\max_\pi Q_\pi(s,a)\tag{12}
\end{equation}
那么有:
这里注意等式左右两边的概念,左边\(V^*(s)\)是个泛概念,无论你什么策略,该值就是最优价值函数。右边\(V_{\pi ^*}(s)\)是指在最优策略情况下取得的奖励值。
我们讨论\(V_{\pi ^*}(s)\)和\(Q_{\pi ^*}(s,a)\)之间的关系。根据前面所述,V函数是Q函数的一个加权平均,那么得到:
现在\(\pi ^*\)是一个最优策略,如果\(V_{\pi ^*}(s) < \max_a Q_{\pi ^*}(s,a)\)则表示V函数并没有达到最大值,策略\(\pi ^*\)还有提高的空间,这与它是最优策略矛盾,因此有:
据此,我们建立最优策略中\(s,s‘\)之间的关系:
这就是贝尔曼最优方程。
这部分是强化学习的基础知识,也可以了解对时序决策、随机优化的一些基本概念。定义了马尔科夫决策过程的策略、价值函数以及最优准则,那么怎么求解最优策略,是最为核心的问题,之后我再给大家讲解一些方法。
原文:https://www.cnblogs.com/souluki/p/13460639.html