由于无论边权怎么修改,树上任意两点之间的\(lca\)是不变的,所以节点\(u,v\)之间的距离总是可以表示成两个节点分别到根节点的距离之和减去2倍的\(lca(u,v)\)到根节点的距离
问题就是边权修改时,如何动态维护所有节点到根节点的距离
如果图为一条链,那么只要使用树状数组就可以实现单点修改,区间查询
所以可以将树按照一定的顺序变成一条链
设\(dfs\)访问顶点的序列为\(vs[maxn]\),每个顶点第一次出现在\(vs[maxn\)中的位置构成\(id[maxn]\)。\(vs\)就是将树变成的链,由于每条边在序列中出现了两次,所以设沿着叶子方向的边权为正,沿根节点方向的边权为负。这样由于正负相消,从根节点\(root\)到任意节点\(u\)的距离为链中\(id[u]\)的前缀和,修改边权时需要修改正、反两条边的边权,所以在\(dfs\)预处理时需要记录每条边转化成的的正、负两条边的编号
例如:
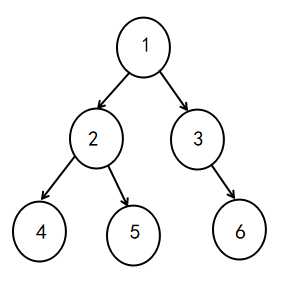
转化成序列:

预处理的时间复杂度\(O(n\log n)\)
两点之间距离查询:计算\(lca\)的时间复杂度\(O(\log n)\),树状数组查询前缀和的时间复杂度\(O(\log n)\)
边权修改:树状数组修改的时间复杂度\(O(\log n)\)
原文:https://www.cnblogs.com/fxq1304/p/13424020.html