时间复杂度:O(nlongn)二分一次需要logn,需要n次
空间复杂度:O(n)需要数组同样大小的临时空间
将数组按照二分法,分成两块,分别各自排顺序
给出如下数组

将两部分分别排好序
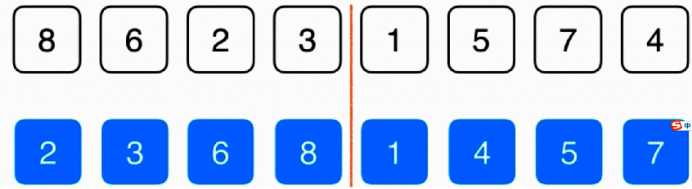
然后用分别排好序的数组

首先,将原数组复制一遍,蓝色箭头表示原数组,红色箭头表示新数组


将复制的数组分成两部分,每一个部分的第一个元素进行比较


![]()
选出小的元素放入原数组,蓝色箭头后移到下一位,选中的红色箭头也后移到下一位

每一轮,红色数组前半部分和后半部分的元素进行比较,将小的元素填入蓝色数组。之后选择下一个元素进入下一轮比较,以此类推
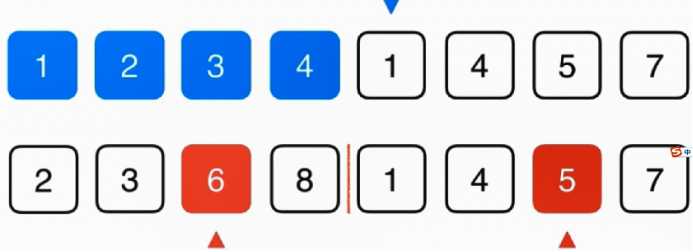
定义三个标记位置
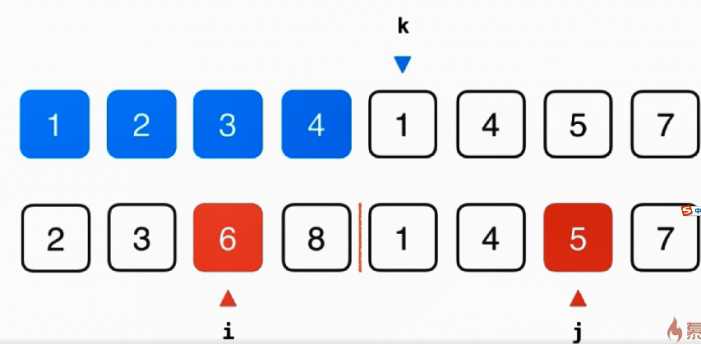
i和j表示需要比较的元素,k表示比较后需要放入的位置
知道了归并的思想,再用递归的方法写归并函数
//将arr[l,mid]和arr[mid+1,r]两部分进行归并 template<typename T> void __merge(T arr[], int l, int mid, int r) {//确定元素放置在原数组中的位置 T aux[r - l + 1]; for(int i=l;i<=r;i++){ aux[i-l] == arr[i]; } int i = l, j = mid + 1; for (int k = l; k <= r; k++) { if(i>mid){//判断是否越界 arr[k] = aux[j-l]; j++; } else if (j > r) {//判断是否越界 arr[k] = aux[i - l]; i++; } else if (aux[i - l] < aux[j - l]) {//如果i-1小,i-1就放入k中 arr[k] = aux[i - l]; i++; } else {//如果j-1小,j-1就放入k中 arr[k] = aux[j - l]; j++; } } } //递归使用归并排序,对arr[l,r]范围进行排序 template <typename T> void __mergeSort(T arr[], int l, int r) { if (l >= r) {//一个元素都没有,数据集为空 return; } int mid = (l + r) / 2; __mergeSort(arr, l, mid);//左半部分归并排序 __mergeSort(arr, mid + 1, r);//右半部分归并排序 __merge(arr, l, mid, r);//归并 } template<typename T> void mergeSort(T arr[], int n) { __mergeSort(arr, 0, n - 1);//第n个是空的,n-1有值 }
原文:https://www.cnblogs.com/ak918xp/p/13413667.html