常见的评估方法有: 1. 留出法(hold-out) 2. 交叉验证法(cross validation)3. 自助法(bootstrap)
将原始数据分成K组(一般是均分),将每个子集数据分别做一次验证集,其余的K-1组子集数据作为训练集,这样会得到K个模型,用这K个模型最终的验证集的分类准确率的平均数作为此K-CV下分类器的性能指标.

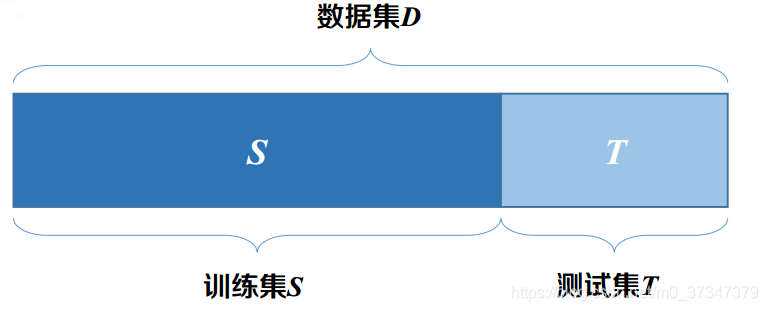
数据集D中包含m个样本,对数据集D进行m次有放回采样,采样到的数据构成数据集D′, 将D′作为训练集,未出现在D′中的数据作为测试集 。
其中样本不出现在D‘中的概率为:
 数据集中约有36.8%的数据不会出现在训练数据集D‘中。
数据集中约有36.8%的数据不会出现在训练数据集D‘中。
注:1. 适用于小数据集。2. 不会减小训练集规模。 3. 改变了数据分布, 易引起估计偏差。
回归模型的任务目标是使得预测值能尽量拟合实际值, 因此常用的性能度量方式主要有绝对误差和均方差两种
MAE误差又称为 L1范数损失(L1-norm loss),即预测点与真实点之间距离之差的绝对值的平均值。能更好地反映预测值误差的实际情况。定义为:
MSE又称为L2范数损失(L2-norm loss),即预测点与真实点之间距离之差平均和的均值。是用来衡量一组数自身的离散程度。定义为:
是观测值与真值偏差的平方和与观测次数m比值的平方根, 是用来衡量观测值同真值之间的偏差。定义为:
分类模型的评估指标比较多,不同的评估指标的侧重点可能不同。
以二分类(正、负)为例:
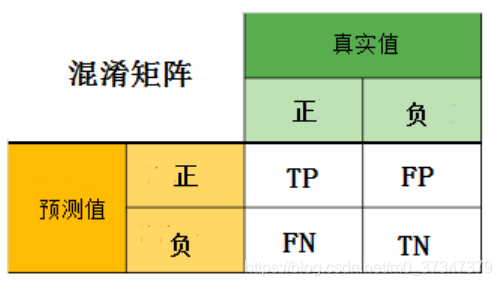
- 真正(TP):模型预测为正的正样本
- 假正(FP):模型预测为正的负样本
- 假负(FN):模型预测为负的正样本
- 真负(TN):模型预测为负的负样本
用来衡量模型对数据集中样本预测正确的比例, 即: 正确预测的正反例数 /总数
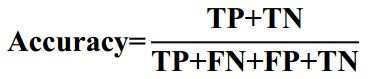
是指所有预测为正例的样本(TP + FP)中真正为正例的样本(TP)的比率, 即: 正确预测的正例数 /预测正例总数
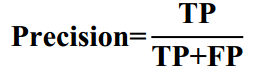
是指所有为正例的样本(TP + FN)中真的正例(TP)的比率, 即: 正确预测的正例数 /实际正例总数
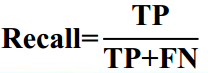
精确率(Precision)和召回率(Recall)评估指标,理想情况下做到两个指标都高当然最好,但一般情况下,Precision高,Recall就低,Recall高,Precision就低。
所以在实际中常常需要根据具体情况做出取舍,例如一般的搜索情况,在保证召回率的条件下,尽量提升精确率。引出了一个新的指标F-score,综合考虑Precision和Recall的调和值F-Score
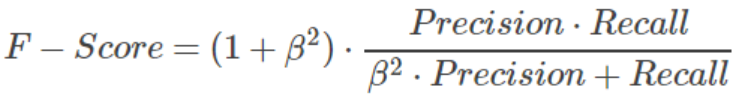
- 当β=1时,称为 F1-score或者 F1-Measure,这时,精确率和召回率都很重要,权重相同。
- 当有些情况下,我们认为精确率更重要些,那就调整β的值小于1,
- 如果我们认为召回率更重要些,那就调整β的值大于1。
根据分类结果计算得到ROC空间中相应的点,连接这些点形成ROC曲线。
真正率(TPR):预测为正的正样本数 /正样本实际数
假正率(FPR) :预测为正的负样本数 /负样本实际数
>
靠近左上角的ROC曲所代表的分类器准确性最高
ROC曲线下的面积(ROC的积分) 称为 AUC。根据曲线位置,把整个图划分成了两部分,曲线下方部分的面积被称为AUC(Area Under Curve),用来表示预测准确性,AUC值越高,也就是曲线下方面积越大,说明预测准确率越高。曲线越接近左上角(X越小,Y越大),预测准确率越高。
- AUC = 1: 100%完美识别正负类,不管阈值怎么设定都能得出完美预测;
- 0.5<AUC<1:优于随机猜测。这个分类器(模型)妥善设定阈值的话,可能有预测价值;
- AUC=0.5:跟随机猜测一样(例:随机丢N次硬币, 正反面的概率为50%), 模型无预测价值;
- AUC<0.5:比随机猜测还差,不存在AUC<0.5的情况
又称为误差矩阵, 主要用于比较分类结果和实例的真实信息
因为聚类是将样本集划分为若干个不相交的子集, 及样本簇, 同样需要通过某些性能度量方式来评估其聚类结果的好坏。直观上看,我们是希望同一簇内的样本能尽可能相似,而不同簇的样本之间尽可能不同。实现这一目标主要有外部指标和内部指标两种方式。
外部指标需要提供一个参考模型,然后将聚类结果与该参数模型进行比较得到一个评判值: 常用的有Jaccard系数、FM指数、Rand指数和标准化互信息
// TODO
原文:https://www.cnblogs.com/magicpig666/p/13405469.html