工作流程

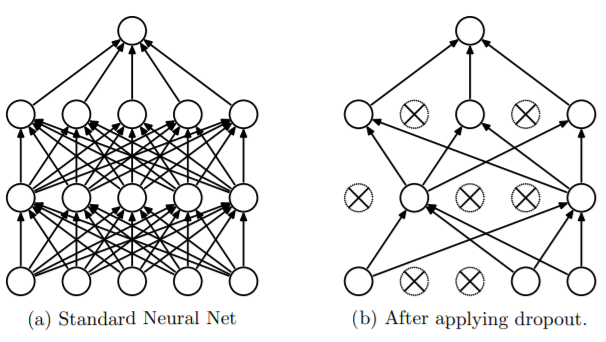
dropout用于解决过拟合，通过在每个batch中删除某些节点(cell)进行训练，从而提高模型训练的效果。

通过随机化一个伯努利分布，然后于输入y进行乘法，将对应位置的cell置零。然后y再去做下一层的前向传播。

这里由于部分cell的缺失，会导致下一层的cell的值偏小，假设一个cell有p的概率被抹除，那么他在网络中发生作用的数学期望是：

所以真正用于网络计算的x的大小只有(1-p)x，而在训练时，dropout会被关闭，所有的cell都会被用于计算（为了避免预测结果的随机性，所以不能有dropout这种随机结构参与运算），相对来说，由于所有的cell都参与了运算，那么下一层的值会更大。为了抵消这种差距，在测试时用 \((1-p)x\) 进行计算。这样cell传递到下一层时，可以使下一层和train时保持在同一个量级上。

如果不想在预测时把x乘上(1-p)，我们可以在训练时把x进行缩放。即 \(\frac{x}{(1-p)}\)，这样在预测时就可以直接用x进行运算，而不用改变x的值。这种方式也被称为 iverse dropout。

为什么可以解决过拟合

1. dropout通过随机去除cell，使得网络的结果在不断的变化当中。可以认为，最后的模型是在多个模型的基础上综合起来的模型。在处理过拟合问题的时候，常常使用多个模型训练一份数据，最后通过“投票”或者取平均的方式来预测，可以降低过拟合的影响。而dropout的这种“综合”的结果就类似多个模型共同来预测。

2. 减少神经元之间的依赖关系。在神经网络中可能两个神经元相互依赖才能产生比较好的效果。比如一个cell很大而另一个很小，它们的组合却不影响最终的结果，但是这些cell学到的并不是正确的知识。

问题

在学习dropout的算法中关于drop的反向传播还有一些细节值得推敲。理论上来说，dropout是的效果是让一个cell在神经网络中消失，不管是前向传播还是反向传播，都要忽略这个cell的存在。但是关于dropout反向传播的具体操作众说纷纭。很难找到一个明确的说法。

1. 由于cell已经被置零，所以在对下一层网络求导时，与之相连的权重的梯度都是零，所以下一层与之相连的权重都不会被更新。
2. cell连接前后两个权重，虽然cell之后的权重可以自动根据cell的值来判断梯度。但是与cell相连的前面的权重就不可以这么做了，所以这些权重需要做一个判断，如果是与cell相连的权重，那么就抹除他的误差。

参考资料：
http://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf
https://blog.csdn.net/program_developer/article/details/80737724
https://blog.csdn.net/oBrightLamp/article/details/84105097

Drop原理分析

原文：https://www.cnblogs.com/twilight0402/p/13396336.html