You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].
Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.
If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.
Example 1:
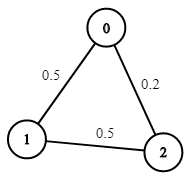
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 Output: 0.25000 Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.
Example 2:
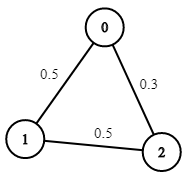
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 Output: 0.30000
Example 3:
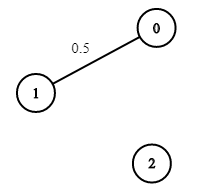
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 Output: 0.00000 Explanation: There is no path between 0 and 2.
Constraints:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1class Node { public int id; public double prob; public Node(int id, double prob) { this.id = id; this.prob = prob; } } class Solution { public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) { Map<Integer, List<Node>> neighbors = new HashMap<>(); for (int i = 0; i < n; i++) { neighbors.put(i, new ArrayList<>()); } for (int i = 0; i < edges.length; i++) { int a = edges[i][0], b = edges[i][1]; double p = succProb[i]; neighbors.get(a).add(new Node(b, p)); neighbors.get(b).add(new Node(a, p)); } Map<Integer, Double> res = new HashMap<>(); Set<Integer> calculated = new HashSet<>(); PriorityQueue<Node> heap = new PriorityQueue<>((n1, n2) -> Double.compare(n2.prob, n1.prob)); heap.add(new Node(start, 1.0)); while (!heap.isEmpty()) { Node cur = heap.poll(); if (calculated.contains(cur.id)) { continue; } res.put(cur.id, cur.prob); calculated.add(cur.id); for (Node nxt : neighbors.get(cur.id)) { double newProb = cur.prob * nxt.prob; if (newProb > res.getOrDefault(nxt.id, 0.0)) { res.put(nxt.id, newProb); heap.add(new Node(nxt.id, newProb)); } } } return res.getOrDefault(end, 0.0); } }
用dijistra算法,此算法包括一个Node class,是要把离start点的node和probability记录下来。
一个map做的graph,一个hashset做的用来保存已经计算过的节点的数组,一个priorityqueue用来永远取得离start点最近(此处为prob最小)的队列,然后bfs
1514. Path with Maximum Probability
原文:https://www.cnblogs.com/wentiliangkaihua/p/13298555.html