动区间最值

时间：2020-07-12 20:04:22 阅读：53 评论：0 收藏：0 [点我收藏+]

已知函数\(f(x)=mx^3+nx^2(n,m\in R,m>n,m\neq 0)\)的图像在\((2,f(2))\)处切线与\(x\)轴平行

\((1)\) 判断\(n,m\)正负

\((2)\) 若函数\(f(x)\)在区间\([n,m]\)上有\(m-n^2\)，求\(m\)的值

解答：

\((1)\)

\[f‘(x)=3mx^2+2nx \]

\[f‘(2)=0 \]

\[12m+4n=0 \]

\[-3m=n \]

\[m>0,n<0 \]

\((2)\)

\[f‘(x)=3mx^2-6mx \]

\[f‘(x)=3mx(x-2) \]

可以推出\(f‘(x)\)的大致函数图像

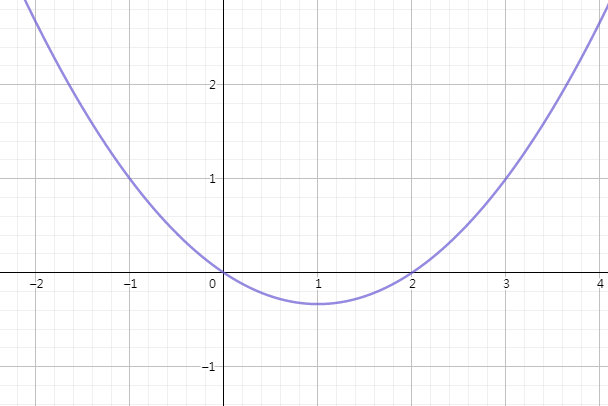
技术分享图片

再结合\(f(x)\)的零点\((0,0),(3,0)\)画出\(f(x)\)大致图像

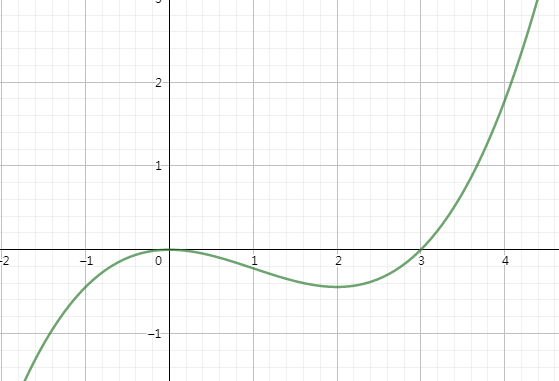
技术分享图片

当\(m\le 3\)时

\[f_{max}(x)=f(0)=0 \]

\[m-n^2=0,-3m=n \]

解出

\[m=\frac{1}{9} \]

当\(m>3\)时

\[f_{max}(x)=f(m)=m^4-3m^3 \]

\[m^4-3m^3=m-n^2 \]

\[m^4-3m^3+9m^2-m=0 \]

\[g(m)=m^3-3m^2+9m-1 \]

\[g‘(m)=3m^2-6m+9 \]

\[g‘(m)=3(m-1)^2+6 \]

所以\(g(m)\)在定义域上单调增

又因为\(g(3)>0\)，所以\(m<3\)，不成立

所以\(m=\frac{1}{9}\)

原文：https://www.cnblogs.com/knife-rose/p/13289461.html

踩

(0)

评论一句话评论（0）

分享档案

更多>