首先,需要了解树这种数据结构的定义:
树:是一类重要的非线性数据结构,是以分支关系定义的层次结构。每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树
树的结构类似现实中的树,一个父节点有若干子节点,而一个子节点又有若干子节点,以此类推。
| 名称 | 含义 |
|---|---|
| 根节点 | 树的顶端结点 |
| 父节点 | 若一个节点含有子节点,则这个节点称为其子节点的父节点 |
| 子节点 | 具有相同父节点的节点 |
| 兄弟节点 | 彼此都拥有同一个父节点的节点 |
| 叶子节点 | 即没有子节点的节点 |
| 节点的权 | 即节点值 |
| 路节点的度 | 一个节点含有的子树的个数 |
| 树的度 | 一棵树中,最大的节点的度称为树的度 |
| 深度 | 根结点到这个结点所经历的边的个数 |
| 层数 | 该节点的深度+1 |
| 高度 | 结点到叶子结点的最长路径所经历的边的个数 |
| 树高度 | 即根节点的高度 |
| 森林 | 由m(m>=0)棵互不相交的树的集合称为森林 |
二叉树就是每个节点最多只有两颗子树的树:
对于二叉树有:
满二叉树:所有的子节点都在最后一层,且节点总数与层数有节点总数=2^n-1
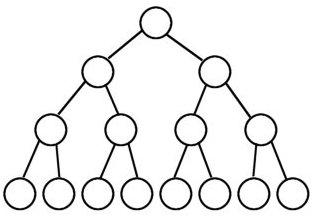
完全二叉树:从根节点到倒数第二层都符合满二叉树,但是最后一层节点不完全充填,叶子结点都靠左对齐

二叉树遍历分为三种:
可见,根据父节点输出顺序即可以判断是哪一种遍历。
先创建节点类:
/**
* @Author:黄成兴
* @Date:2020-07-11 17:30
* @Description:二叉树
*/
public class BinaryTreeNode {
private int nodeNum;
/**
* 右子节点
*/
private BinaryTreeNode right;
/**
* 左子节点
*/
private BinaryTreeNode left;
public BinaryTreeNode(int nodeNum) {
this.nodeNum = nodeNum;
}
@Override
public String toString() {
return "BinaryTreeNode{" +
"nodeNum=" + nodeNum +
‘}‘;
}
public int getNodeNum() {
return nodeNum;
}
public void setNodeNum(int nodeNum) {
this.nodeNum = nodeNum;
}
public BinaryTreeNode getRight() {
return right;
}
public void setRight(BinaryTreeNode right) {
this.right = right;
}
public BinaryTreeNode getLeft() {
return left;
}
public void setLeft(BinaryTreeNode left) {
this.left = left;
}
}
实现遍历方法:
/**
* @Author:黄成兴
* @Date:2020-07-11 17:44
* @Description:二叉树
*/
public class BinaryTree {
private BinaryTreeNode root;
public BinaryTree(BinaryTreeNode root) {
if (root == null) {
throw new RuntimeException("根节点不允许为空!");
}
this.root = root;
}
public void preOrder(){
preOrder(root);
}
/**
* 前序遍历
*/
public void preOrder(BinaryTreeNode node){
//打印节点
System.out.println(node);
//向左子树前序遍历
if (node.getLeft() != null) {
preOrder(node.getLeft());
}
//向右子树前序遍历
if (node.getRight() != null) {
preOrder(node.getRight());
}
}
public void inOrder(){
inOrder(root);
}
/**
* 中序遍历
*/
public void inOrder(BinaryTreeNode node){
//向左子树中序遍历
if (node.getLeft() != null) {
inOrder(node.getLeft());
}
//打印节点
System.out.println(node);
//向右子树中序遍历
if (node.getRight() != null) {
inOrder(node.getRight());
}
}
public void postOrder(){
postOrder(root);
}
/**
* 后序遍历
*/
public void postOrder(BinaryTreeNode node){
//向左子树中序遍历
if (node.getLeft() != null) {
postOrder(node.getLeft());
}
//向右子树中序遍历
if (node.getRight() != null) {
postOrder(node.getRight());
}
//打印节点
System.out.println(node);
}
}
对含有7个简单的满二叉树进行遍历的结果:

前序遍历:
BinaryTreeNode{nodeNum=1}
BinaryTreeNode{nodeNum=2}
BinaryTreeNode{nodeNum=4}
BinaryTreeNode{nodeNum=5}
BinaryTreeNode{nodeNum=3}
BinaryTreeNode{nodeNum=6}
BinaryTreeNode{nodeNum=7}
中序遍历:
BinaryTreeNode{nodeNum=4}
BinaryTreeNode{nodeNum=2}
BinaryTreeNode{nodeNum=5}
BinaryTreeNode{nodeNum=1}
BinaryTreeNode{nodeNum=6}
BinaryTreeNode{nodeNum=3}
BinaryTreeNode{nodeNum=7}
后序遍历:
BinaryTreeNode{nodeNum=4}
BinaryTreeNode{nodeNum=5}
BinaryTreeNode{nodeNum=2}
BinaryTreeNode{nodeNum=6}
BinaryTreeNode{nodeNum=7}
BinaryTreeNode{nodeNum=3}
BinaryTreeNode{nodeNum=1}
大体逻辑同遍历,这里就不在赘述了,直接放代码:
/**
* 前序查找
* @param num
* @param node
* @return
*/
public BinaryTreeNode preSearch(int num,BinaryTreeNode node){
BinaryTreeNode result = null;
//判断当前节点是否为查找节点
if (node.getNodeNum() == num) {
result = node;
}
//判断左节点是否为空,不为空就前序查找节点
if (node.getLeft() != null) {
result = preSearch(num, node.getLeft());
}
//如果左树找到就返回
if (result != null){
return result;
}
//否则就判断并递归前序查找右树
if (node.getRight() != null) {
result = preSearch(num, node.getRight());
}
return result;
}
/**
* 中序查找
* @param num
* @param node
* @return
*/
public BinaryTreeNode inSearch(int num,BinaryTreeNode node){
BinaryTreeNode result = null;
//判断左节点是否为空,不为空就中序查找节点
if (node.getLeft() != null) {
result = inSearch(num, node.getLeft());
}
//如果左树找到就返回
if (result != null){
return result;
}
//如果左树未找到就判断当前节点是不是
if (node.getNodeNum() == num) {
result = node;
}
//否则就判断并递归前序查找右树
if (node.getRight() != null) {
result = inSearch(num, node.getRight());
}
return result;
}
/**
* 后序查找
* @param num
* @param node
* @return
*/
public BinaryTreeNode postSearch(int num,BinaryTreeNode node){
BinaryTreeNode result = null;
//判断左节点是否为空,不为空就后序查找节点
if (node.getLeft() != null) {
result = postSearch(num, node.getLeft());
}
//如果左树找到就返回
if (result != null){
return result;
}
//否则就判断并递归后序查找右树
if (node.getRight() != null) {
result = postSearch(num, node.getRight());
}
//判断右树是否找到
if (result != null){
return result;
}
//如果右树仍未找到就判断当前节点是不是
if (node.getNodeNum() == num) {
result = node;
}
return result;
}
对于二叉树的删除,有以下逻辑:
/**
* 删除节点
* @param num
* @param node
* @return
*/
public void delete(int num, BinaryTreeNode node) {
//判断删除的是否为根节点
if (root.getNodeNum() == num) {
throw new RuntimeException("不允许删除根节点!");
}
//如果子节点就是要删除的节点
if (node.getLeft() != null && node.getLeft().getNodeNum() == num) {
node.setLeft(null);
return;
}
if (node.getRight() != null && node.getRight().getNodeNum() == num) {
node.setRight(null);
return;
}
//否则就往左树或右树遍历直到找到或遍历完为止
if (node.getLeft() != null) {
delete(num, node.getLeft());
}
if (node.getRight() != null) {
delete(num,node.getRight());
}
}
原文:https://www.cnblogs.com/Createsequence/p/13288190.html