二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回 L 和 R（含）之间的所有结点的值的和。

二叉搜索树保证具有唯一的值。

示例 1：

输入：root = [10,5,15,3,7,null,18], L = 7, R = 15
输出：32

示例 2：

输入：root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10
输出：23

提示：

1. 树中的结点数量最多为 10000 个。
2. 最终的答案保证小于 2^31。

解答：

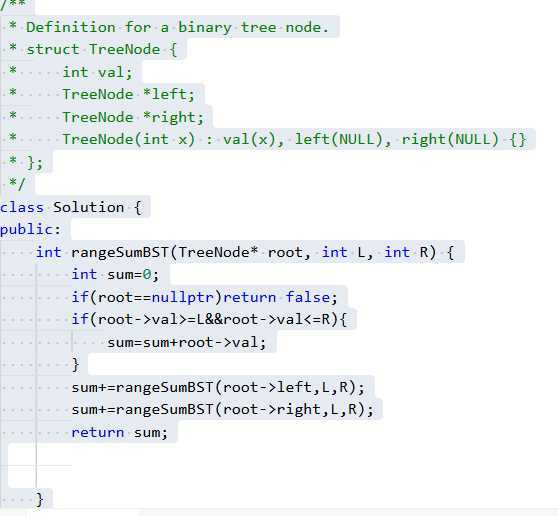
题目主要通过递归来实现，递归的结果为输出的总和；

题目通过递归实现比较简单，输出求和不是 L 和 R 节点之间的所有连接结点的总和，而是符合 L <= val <= R 的所有节点的总和，即例子 1 中 32 = 7 + 10 + 15，值为10的结点是处于L和R之间的结点；同理， 例子 2 中 23 = 6 + 7 + 10。

二叉搜索树的特点为：若左子树不为空, 则左子树的所有结点都小于根节点; 若右子树不为空, 则右子树的所有结点都大于根节点。

若该结点的值 val 处于 L 和 R 之间，则将该值加起来；若 val < L，根据二叉搜索树的特点，该结点的右边可能存在符号条件的值，继续搜寻该结点的右边；若 val > R，该结点的左边可能存在符号条件的值，继续搜寻该结点的左边。

	public int rangeSumBST(TreeNode root, int L, int R) {
	    if(root == null) return 0;
	    if(root.val >= L && root.val <= R){
	    	return root.val + rangeSumBST(root.left, L, R) + rangeSumBST(root.right, L, R);
	    }else if(root.val < L){
	    	return rangeSumBST(root.right, L, R);
	    }else{//root.val > R
	    	return rangeSumBST(root.left, L, R);
	    }
    }