Codeforces Round #515 (Div. 3) E. Binary Numbers AND Sum (二进制,前缀和)

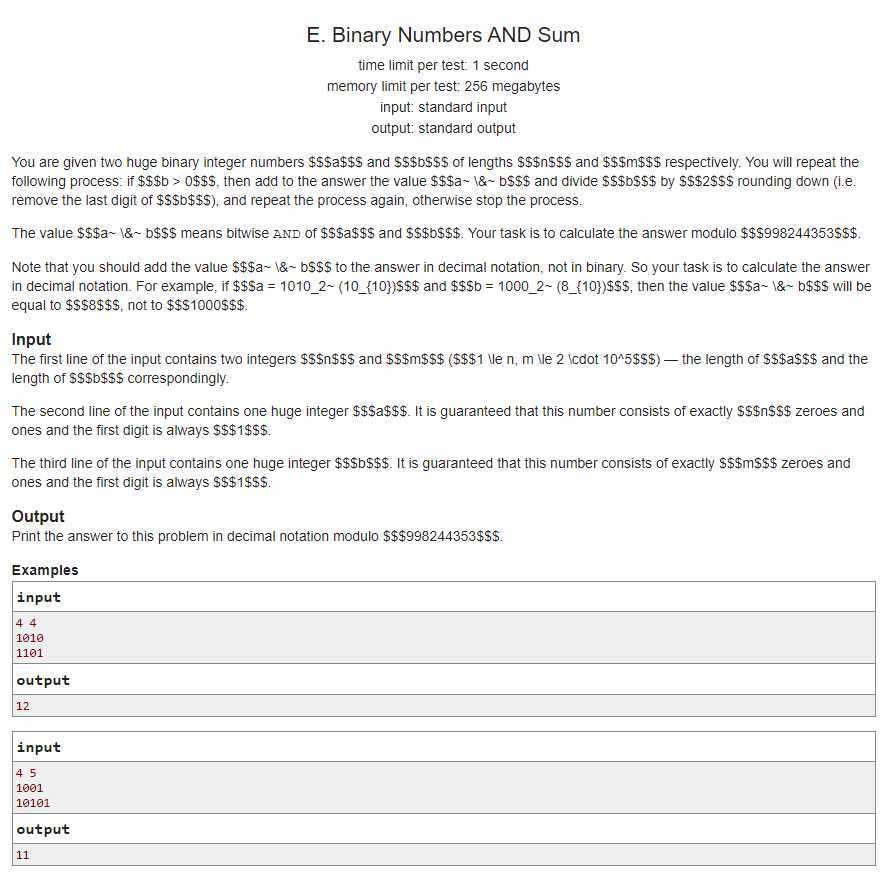
• 题意:有两个\(01\)字符串\(a\)和\(b\),每次让\(a\)和\(b\)进行与运算,将值贡献给答案,然后将\(b\)右移一位,直到\(b=0\).

• 题解:因为\(a\)不变,而\(b\)每次右移一位,所以我们看\(b\)中\(1\)的位置在\(a\)中所对应的位置,从该位置到最低位,所有为\(1\)的位置都要算一次十进制的数贡献给答案,那么为了降低复杂度,很明显,我们使用前缀和,用十进制记录\(a\)中从低位到高位的和,然后再从低位到高位遍历\(b\),累加所有\(1\)位置在\(a\)所对应的前缀和.

• 代码:

  int n,m;
  string a,b;
  ll v[N];
   
  ll fpow(ll a,ll k){
  	ll res=1;
  	 while(k){
  	 	if(k&1) res=res%mod*a%mod;
  	 	a=a*a%mod;
  	 	k>>=1;
  	 }
  	 return res;
  }
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
    	cin>>n>>m;
    	cin>>a>>b;
    	reverse(a.begin(),a.end());
    	reverse(b.begin(),b.end());
    	 for(int i=0;i<n;++i){
    	 	if(a[i]==‘1‘){
    	 		v[i]=fpow(2,i);
    	 	}
    	 }
    	 for(int i=0;i<m;++i){
    	 	v[i]+=v[i-1];
    	 }
    	 ll ans=0;
    	 for(int i=0;i<m;++i){
    	 	if(b[i]==‘1‘){
    	 		ans+=v[i];
    	 		ans%=mod;
    	 	}
    	 }
  
    	 cout<<ans<<endl;
  
      return 0;
  }
  

Codeforces Round #515 (Div. 3) E. Binary Numbers AND Sum (二进制,前缀和)

原文：https://www.cnblogs.com/lr599909928/p/13286001.html