在棋盘上,从点(0,0)走到(i,j)的方案数是C(i+j,i)。
问题:求从点(0,1)走到点(i,j)且不接触直线y=x的路径方案数。
我们可以取(i,j)关于直线y=x的对称点(j,i),可以发现每一条从(0,1)出发到(i,j)且接触了直线y=x的路径都对应了一条从(0,1)出发到(j,i)的路径,我们只需要把这条路径在最后一次接触直线后的那部分沿y=x翻折即可建立起这样一种对应关系。然后我们将从(0,1)到(i,j)任意走的方案数减去接触了直线的不合法方案数(即从(0,1)到(j,i)的方案数)即可得到合法方案数。 这个方案数为:\(C(i+j-1,i)-C(i+j-1,i-1)\)
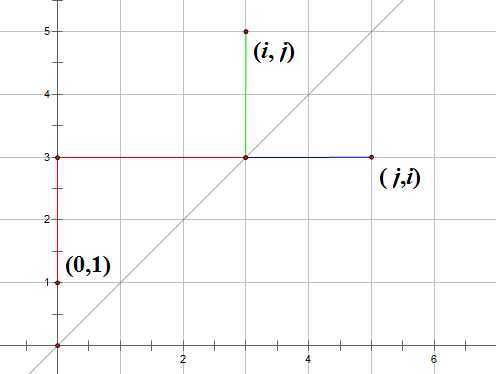
问题:从(0,0)出发到(i,j)且不穿过直线y=x的方案数。
这时不穿过直线y=x等价于不接触直线y=x-1,所有我们取(i,j)关于直线y=x-1的对称点(j+1,i-1),那么每条不合法的路径就对应了一条从(0,0)到(j+1,i-1)的路径,那么我们就可以算出合法路径数为:\(C(i+j,i)-C(i+j,i-1)\)
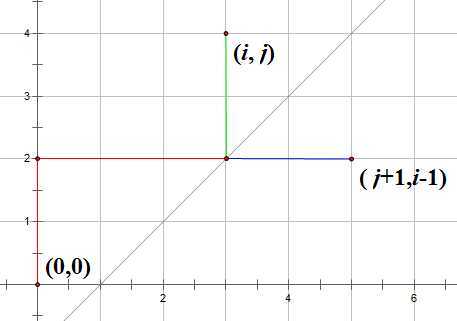
总结:其实我们就是要把接触了边界直线的一条路径对应成目标点关于边界直线对称的那个点的一条路径。
?
?
原文:https://www.cnblogs.com/lishuyu2003/p/13285433.html