设\(f(x),g(x)\)是定义在\(R\)上的两个周期函数
\(f(x)\)的周期为\(4\),\(g(x)\)的周期为\(2\),且\(f(x)\)是奇函数
当\(x\in (0,2]\)时,\(f(x)=\sqrt{1-(x-1)^2}\)
\(g(x)=\begin{cases}k(x+2)&0<x\le 1\\-\frac{1}{2}&1<x\le 2\end{cases}\)
其中\(k>\),若方程在\((0,9]\)上恰好有\(8\)个零点,求\(k\)取值范围
根据\(f(x)\)的解析式和奇函数可以得出
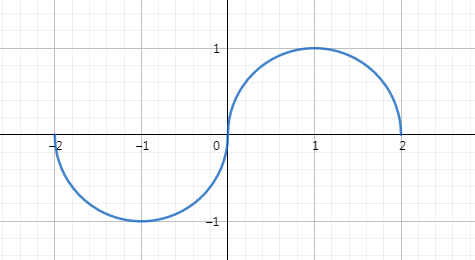
再根据周期得到
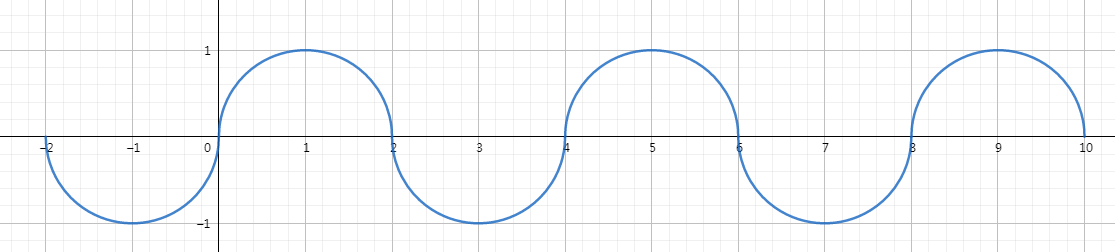
再考虑\(g(x)\),先算出常数段交点个数

发现一共有\(2\)个交点,那么剩下部分应该和\(g(x)\)共有\(6\)个交点,即每个\((0+k,1+k],k\in Z\)之间应该有两个交点
那么\(g(x)\)的第一段函数应该处在两条红线之间

可以解出\(k\in[\frac{1}{3},\frac{\sqrt{2}}{4})\)
原文:https://www.cnblogs.com/knife-rose/p/13283286.html