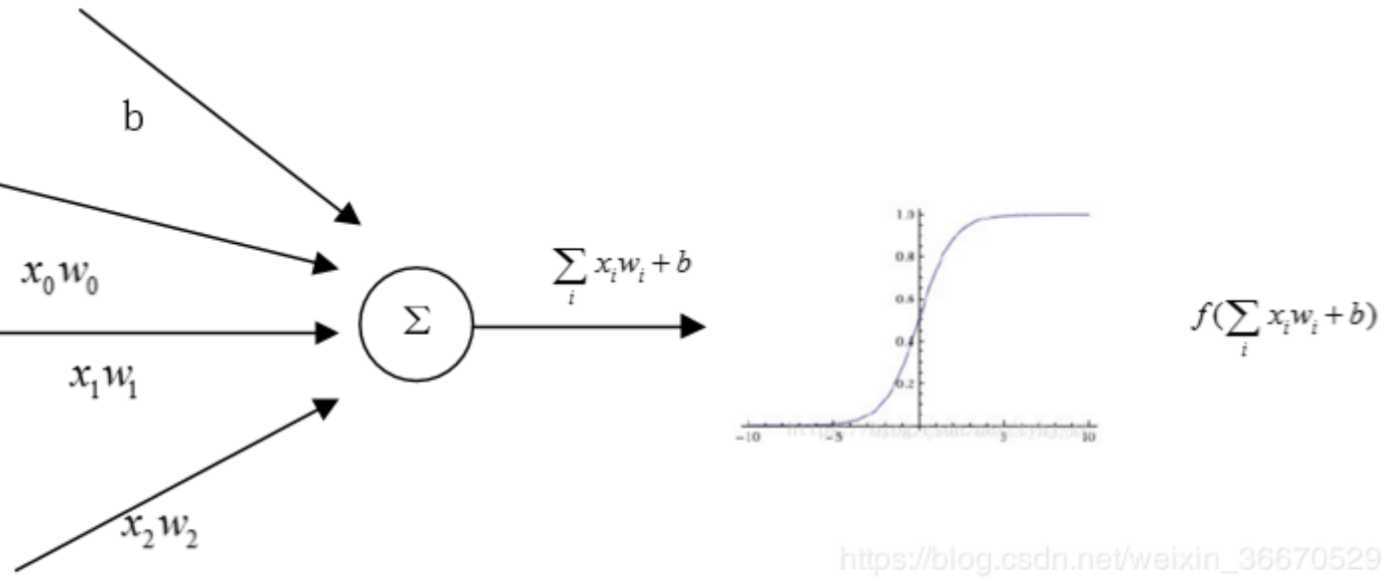
一层神经网络的数学形式很简单,可以看成是一个线性运算再加上一个激活函数,那么激活函数的作用是什么?
答:激活函数的作用是加入非线性因素,提高神经网络对模型的表达能力,解决线性模型不能解决的问题。举个例子:将一层神经网络用作分类器,正样本就让激活函数激活变大,负样本让激活函数激活变小,最终实现对正负样本的划分。
二、常见的激活函数及其优缺点
①、Sigmoid函数
$f\left ( z \right )=\frac{1}{1+e^{-z}}$
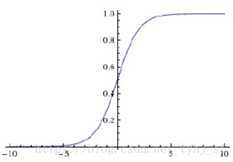
特点:能将实数输入转化到0~1之间的输出,即越大的负数输出为0,越大的正数输出为1,故具有很好的解释性
缺点:①、Sigmoid函数会造成梯度消失。如上图,在sigmoid函数靠近正/负无穷时,梯度会变成0。梯度下降法是通过学习率乘上梯度来更新参数,因此如果梯度接近0,那么参数将无法更新,造成模型不会收敛。并且使用sigmoid函数时,初始化权重不能太大,否则否则线性运算后经激活函数,大多神经院还是没有办法更新参数,所以权重初始化在[0,1]。
②、sigmoid输出不是以0为均值的,那么下一层网络的输入是非0均值,如果输入到下一个神经元的全是正的,这会导致梯度全是正的,更新参数后也永远是正梯度。比如$f\left ( x \right )=w^{T}x+b$,这时候$\bigtriangledown f\left ( w \right )=x$,如果x是均值为0的数据,那么梯度就会有正有负。
②、Tanh函数
$tanh\left ( x \right )=2sigmoid\left ( 2x \right )-1$,Tanh函数是Sigmoid函数的变形
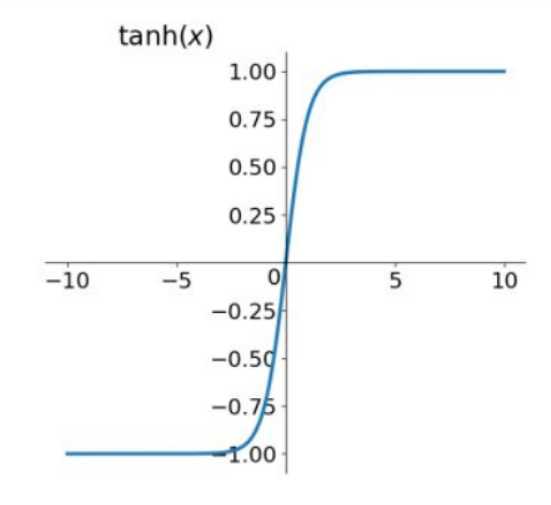
从图上可以看出,它将输入的数据转化为-1~1之间,均值变成了0,解决了sigmoid的第二个问题,因此tanh函数比sigmoid函数更好,但是仍存在梯度消失的问题。
原文:https://www.cnblogs.com/xiazhenbin/p/13262238.html