《流形优化方法求解约束问题》

时间：2020-07-07 15:24:53 阅读：136 评论：0 收藏：0 [点我收藏+]

最近几年，流形优化方法（或者叫黎曼优化）算是比较热门的，它提供了一个新的角度去求解和分析一类特殊的约束优化问题，也就是流形约束优化问题。

这篇文章的目的是让大家对这个方向有个大概的理解。详细的入门书籍建议看【1】【2】

另外综述文章看【3】还有一些博士论文：【4】【5】.

一句话概括就是：传统的优化方法是在欧氏空间考虑问题，而流形优化是在黎曼流形中考虑问题，这个黎曼流形哪来的呢？约束给的！也就是把欧氏空间的约束看成是一个流形。

一、流形约束问题

1.问题阐述

流形约束优化问题是指一类特殊的约束优化问题，它的约束具有流形结构。考虑一般的问题：

$技术分享图片$ 其中 $技术分享图片$ 表示流形约束。这个问题你可以简单的把它看成是约束问题，然后用传统的一些针对约束优化问题的优化方法去求，比如罚方法，增广拉格朗日方法等等。为什么有了这些方法还有去弄个流形优化方法出来，因为首先流行约束通常非凸，收敛性很难保证，其次这些方法不能保证迭代点总是满足约束，最后，流形约束是有结构的，这些方法没有去探索这些结构信息。以上说的三点正是流形优化的三个优点：

所有迭代点保持约束可行性，也就是总是在流形 $技术分享图片$ 上。
流形优化将问题（1）理解为流形上的无约束优化问题，便于分析收敛性。
利用了流形约束本身的结构信息。

2.流形约束的例子

接下来介绍一下常见的 $技术分享图片$ 有哪些

Stiefel manifold: $技术分享图片$
Grassmann manifold: $技术分享图片$ :all $技术分享图片$ -dimensional subspaces of $技术分享图片$
Symmetric positive definite manifold: $技术分享图片$
Fixed-rank manifold: $技术分享图片$

3.问题的例子

稀疏主成分分析

$技术分享图片$

Finding the sparsest vector in subspace

$技术分享图片$

典型相关性分析

$技术分享图片$

鲁棒低秩矩阵恢复

$技术分享图片$

二、预备知识

在欧氏空间中的优化方法已经很成熟，对于在流形上设计优化方法，一切在欧氏空间中看起来理所应当的东西在黎曼流形上却不成立，因此我们需要重新定义。

1.黎曼流形

引用wen huang的一句话解释：

"Roughly, a Riemannian manifold $技术分享图片$ is a smooth set with a smoothly-varying inner product on the tangent spaces."

2.黎曼梯度

因为我们要设计优化方法，梯度是最重要的，我们要定义流形上的梯度，称为黎曼梯度，并且限制在切空间上。

Riemannian Gradient: $技术分享图片$ is denoted as the unique tangent vector satisfying

$技术分享图片$

为什么要在切空间上考虑梯度，因为切空间是线性子空间，性质好。可以将切空间理解为流形在某个点的线性逼近，因此只要邻域足够小，切空间和流形的差可以得到控制。

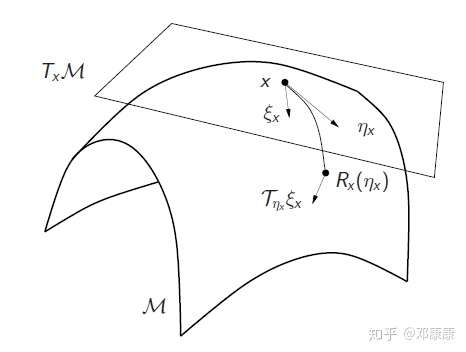
3.收缩算子

有了负梯度，接下来是怎么往前走一步，假设我们有了 $技术分享图片$ ，和该点的黎曼梯度： $技术分享图片$ ，我们如何得到 $技术分享图片$ ，如果是像欧氏空间一样：

$技术分享图片$ 这不能保证迭代点还在流形上，也就是说不满足约束条件。因此我们定义流形上的”加法“：

Retraction：A retraction on a manifold $技术分享图片$ is a smooth mapping $技术分享图片$ with the following properties. Let $技术分享图片$ denote be the restriction of $R$ to $技术分享图片$ ：

$技术分享图片$ , where $技术分享图片$ the zero element of $技术分享图片$
$技术分享图片$ ,where $技术分享图片$ is the identity mapping on $技术分享图片$

对于不同的流形有不同的收缩算子，并且对于某个流形可以有多个算子。在欧氏空间中，收缩算子就是传统意义下的加法。

有了这两个定义，我们就可以很轻松的设计出黎曼梯度方法，基本迭代为：

$技术分享图片$

我们来比较下传统梯度和黎曼梯度的区别：

4.向量转移算子

在黎曼流形中，不同点的梯度位于该点的切空间上，那么问题来了，不同点的黎曼梯度如何去比较？比如 $技术分享图片$ 和 $技术分享图片$ ,这两个不在同一个切空间上。这里的解决方案是，我们把其中一个”平移“到另一个的切空间上。于是有了这个算子：

这个算子在共轭梯度方法中会用到。

vector transport

三、流形优化方法

1.黎曼梯度方法

$技术分享图片$

和传统梯度方法一样，其中的步长可以有不同的选择，比如线搜索，BB步长等

2.黎曼共轭梯度

$技术分享图片$

注意到第二步，因为 $技术分享图片$ 和 $技术分享图片$ 不在同一个切空间上，没办法作比较，所以我们对 $技术分享图片$ 用了向量转移算子，使得他们保持在同一个切空间。

二阶方法比较复杂一点，下次再补上。

四、总结

流形优化用于求解一类约束优化问题，将欧氏空间中的约束优化问题转化为黎曼流形上的无约束优化问题。关于欧氏空间下优化理论的很多东西都能扩展过来，比如函数的凸性，光滑性等等。

流形优化方法并不能求解所有的约束优化，只限于那些可以看成是黎曼流形的约束，比如前面提到的正交约束，对称正定约束，低秩约束等等。
欧氏空间的临近类算法不太好扩展到黎曼流形，至少在计算方面，因为在欧氏空间下“临近友好”这个性质扩展到黎曼流形下就没有了。

黎曼优化?zhuanlan.zhihu.com 技术分享图片

参考文献

【1】 Absil, P-A., Robert Mahony, and Rodolphe Sepulchre.Optimization algorithms on matrix manifolds. Princeton University Press, 2009.

【2】Nicolas Boumal. An introduction to optimization on smooth manifolds. 2020.

【3】Hu, Jiang, Xin Liu, Zai-Wen Wen, and Ya-Xiang Yuan. "A brief introduction to manifold optimization."Journal of the Operations Research Society of China(2019): 1-50.

【4】Zhang, Hongyi. "Topics in non-convex optimization and learning." PhD diss., Massachusetts Institute of Technology, 2019.

【5】Huang, Wen. "Optimization algorithms on Riemannian manifolds with applications." (2013).

编辑于 6 小时前