假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
class Solution {
public:
int climbStairs(int n) {
if(n <= 1)
return n;
int* dp = new int[n+1]; //注意这里new分配空间
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
for(int i=3;i<=n; i++){
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
};
优化版本:
class Solution {
public:
int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
};
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
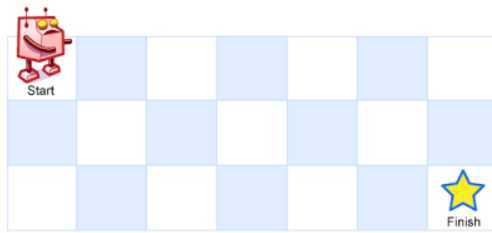
例如,上图是一个7 x 3 的网格。有多少可能的路径?
class Solution {
public:
int uniquePaths(int m, int n) {
if(m<=0 || n<=0){
return 0;
}
vector<vector<int>> dp(m,vector<int>(n, 0));
for(int i=0; i<m;i++){
dp[i][0] = 1;
}
for(int j=0;j<n;j++){
dp[0][j] = 1;
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j] = dp[i-1][j]+dp[i][j-1];
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
return dp[m-1][n-1];
}
};
优化:
原文:https://www.cnblogs.com/bailuoxi/p/13222565.html