
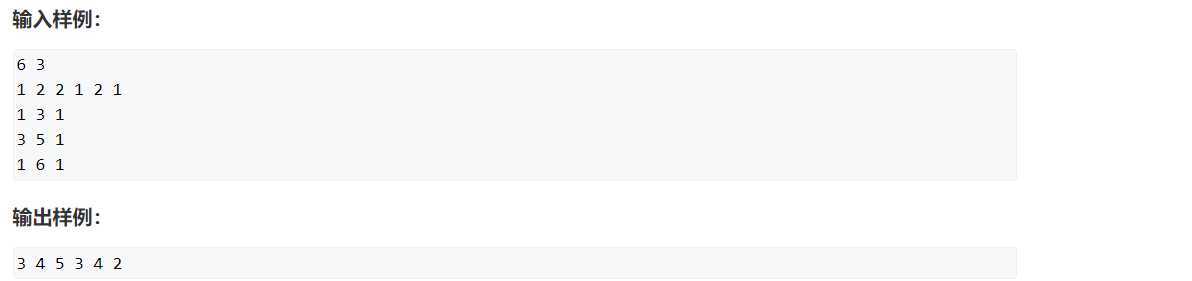
差分是前缀和的逆运算
假如原数组是a[1],a[2],...,a[n].
我们构造b数组,b[1],b[2],...,b[n].
使得a[i] = b[1] + b[2] + ... + b[i]
使得a数组是b数组的前缀和
b数组就称为a数组的差分
差分的作用:
对b数组求一遍前缀和就可以得出a数组
将b[l]加上c之后,从a[l],a[l + 1]一直到a[n]都会加上c
再将b[r + 1]减去c
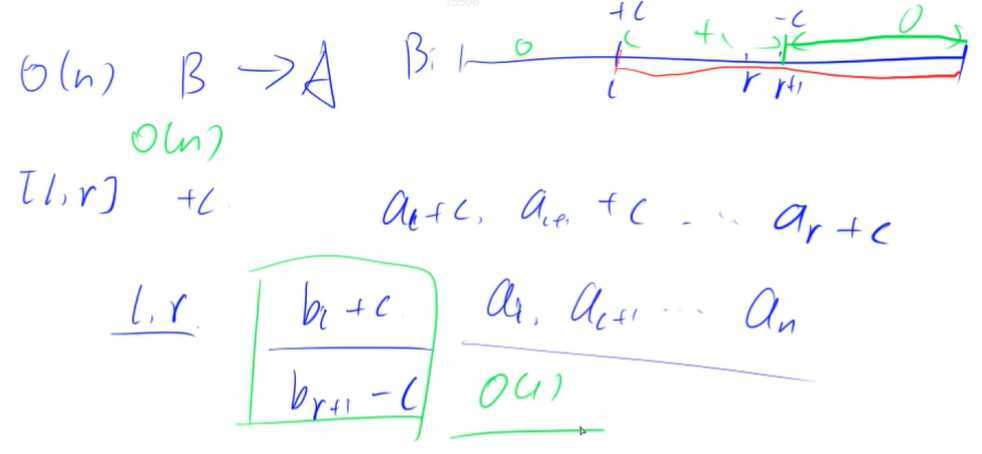
然后就是初始化问题。
开始时我们假定a数组全部都是0,那差分数组b也全部都是0
然后我们看成是对a数组进行了n次插入操作
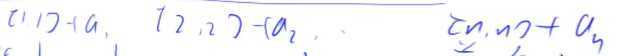
也就是说,如果我们想把区间[l, r]整个加上一个数c的话,就让b[l] + c,b[r + 1] - c即可。

1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 100010; 4 int a[N], b[N]; 5 //a是原数组 6 //b是差分数组 7 void insert(int l, int r, int c) { //在[l, r]之间加上c 8 b[l] += c; 9 b[r + 1] -= c; 10 } 11 int main() { 12 int n, m; 13 cin >> n >> m; 14 for (int i = 1; i <= n; i++) { 15 cin >> a[i]; 16 insert(i, i, a[i]); //构造b数组 17 } 18 while (m--) { 19 int l, r, c; 20 cin >> l >> r >> c; 21 insert(l, r, c); 22 } 23 for (int i = 1; i <= n; i++) { //求所有操作后的数组,就是求一遍前缀和 24 b[i] += b[i - 1]; 25 cout << b[i] << " "; 26 } 27 return 0; 28 }
原文:https://www.cnblogs.com/fx1998/p/12821785.html