[编程题]构建乘积数组

7、构建乘积数组[????]

题目：

给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]A[1]...A[i-1]A[i+1]...A[n-1]。不能使用除法。（注意：规定B[0] = A[1] * A[2] * ... * A[n-1]，B[n-1] = A[0] * A[1] * ... * A[n-2];）

package jianzhioffer;

import java.util.Arrays;

/**
 * @author jiyongjia
 * @create 2020/6/20 - 0:25
 * @descp: 构建乘积数组
 *
 * 给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。
 * （注意：规定B[0] = A[1] * A[2] * ... * A[n-1]，B[n-1] = A[0] * A[1] * ... * A[n-2];）
 *
 * 本质：就是B[i]就是A数组中除了A[i]在外的所有数相乘
 */
public class P7_multiplyArray {
    public static void main(String[] args) {
        int[] ints = {1, 2, 3, 4};
        int[] multiply = multiply(ints);
        System.out.println(Arrays.toString(multiply));   //输出：[24, 12, 8, 6]
    }


    public static int[] multiply(int[] A) {
        //A[i]的前缀乘积表达式  mul_pre[i] = A[0]*A[1]*A[2]*A[3]....A[i-1]；
        // A[i]的后缀乘积表达式  mul_post[i] = A[i+1]*A[i+2]*A[i+3]*....A[n-1]；
        //B[i] = mul_pre[i] * mul_post[i]
        int[] B = new int[A.length];

        //计算B数组值
        for (int i = 0; i < B.length; i++) {
            B[i] = pre_mul(i,A)*post_mul(i,A);
        }
        return B;
    }

    //1 前缀乘积表达式：A[i]的前缀乘积表达式 res: A[i] = A[0]*A[1]*A[2]*A[3]....A[i-1]；
    public static int pre_mul(int j,int[] A){
        int[] resPre = new int[A.length];
        //1、如果j=0的情况，前缀乘积就指定为1
        int res_pre = 1;
        if (j==0) {
            res_pre = 1;
            resPre[j] = res_pre;   //存储在结果数组中
        //2、如果j!=0的i情况，都可以进行计算累乘
        }else{
            for (int i = 0; i <= j-1; i++) {
                res_pre *= A[i];
            }
            //累乘之后，把结果存储进去到相应的j的位置
            resPre[j] = res_pre; //存储到结果数组中
        }
        //返回本次调用的结果值
        return resPre[j];
    }


    //2 后缀乘积表达式：A[i]的前缀乘积表达式 res: A[i] = A[i+1]*A[i+2]*A[i+3]*....A[n-1]；
    public static int post_mul(int j,int[] A){
        int[] resPost = new int[A.length];
        //1、如果j=0的情况，前缀乘积就指定为1
        int res_pre = 1;
        if (j==A.length-1) {
            res_pre = 1;
            resPost[j] = res_pre;   //存储在结果数组中
            //2、如果j!=A.length-1的情况，都可以进行计算累乘
        }else{
            for (int i = A.length-1; i >= j+1; i--) {
                res_pre *= A[i];
            }
            //累乘之后，把结果存储进去到相应的j的位置
            resPost[j] = res_pre; //存储到结果数组中
        }
        //返回本次调用的结果值
        return resPost[j];
    }
}

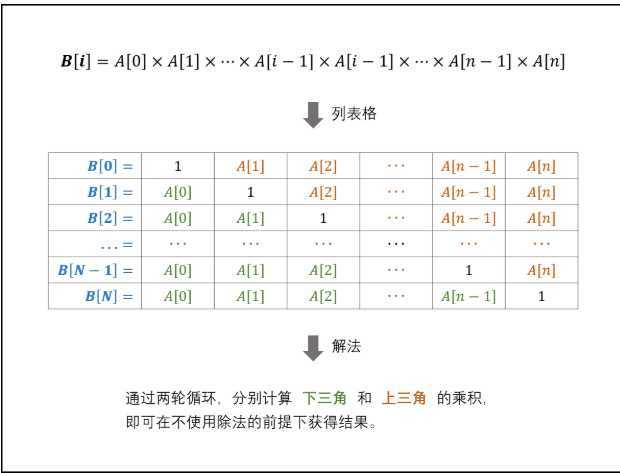
方法2：

public static int[] multiply(int[] A) {
        //A[i]的前缀乘积表达式  mul_pre[i] = A[0]*A[1]*A[2]*A[3]....A[i-1]；
        // A[i]的后缀乘积表达式  mul_post[i] = A[i+1]*A[i+2]*A[i+3]*....A[n-1]；
        //B[i] = mul_pre[i] * mul_post[i]

        int n = A.length;
        int[] B = new int[n];
        //先计算下三角形
        for (int i = 0, p = 1; i < n; i++) {
            //计算左值
            B[i] = p;
            p *= A[i];
        }

        //计算上三角形
        for (int i = n - 1, p = 1; i >= 0; i--) {
            //计算右值
            B[i] *= p;
            p *= A[i];
        }
        return B;
    }

分析执行过程例子：

如：[1,2,3,4]

//下三角形 (计算出左边的累乘积)
B[0] = p = 1
p=p*A[0]= 1*1=1

B[1] = p = p*A[0]= 1*1=1
p=p*A[1]= p*A[0]*A[1] = 1*1*2 = 2

B[2] = p =  p*A[0]*A[1] = 1*1*2 = 2
p=p*A[2] = p*A[0]*A[1]*A[2] = 1*1*2*3 = 6

B[3] = p = p*A[2] = p*A[0]*A[1]*A[2] = 1*1*2*3 = 6
p= p*A[3] = p*A[0]*A[1]*A[2]*A[3] = 1*1*2*3*4 = 24;

//计算下三角形（在左累乘积的基础从下往上乘右边的,此时for中p=1）
B[3] = B[3]*p = 6*1 = 6
p = p*A[3] = 1*4 =4

B[2] = B[2]*p = 2*p =2*4 = 8
p=p*A[2] = 4*3=12

B[1] = B[1]*p = 1*12 = 12;
p=p*A[1] = 12*2 = 24;

B[0] = B[0]*p = 1*24 = 24;
p= p*A[0] = 24*1 = 24

最终：
B = [24,12,8,6]

[编程题]构建乘积数组

原文：https://www.cnblogs.com/jiyongjia/p/13191840.html