上篇文章介绍了二分查找算法。因为二分查找底层依赖的是数组随机访问的特性,所以只能用数组来实现。那么数据存储在链表中,就不能用二分查找算法吗?
对于一个单链表,即便链表中存储的数据是有序的,如果要查找某个数据,也只能从头到尾遍历链表。这样查找效率很低,时间复杂度是O(n)。
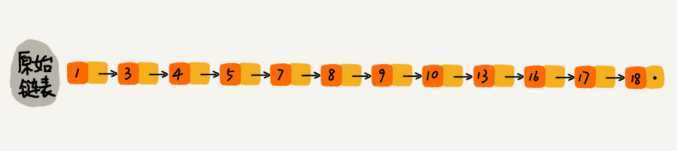
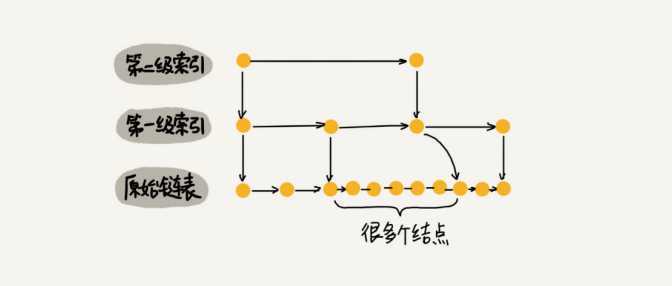
如果像图中那样,对链表建立一级“索引”,查找起来是不是就能更快些呢?每两个结点提取一个结点到上一级,把抽出来的那一级叫作索引或索引层。
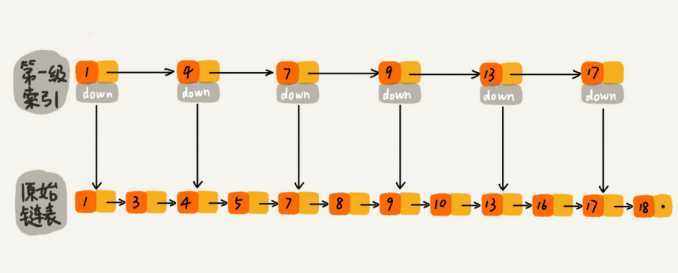
如果要查找某个结点,比如16。原来单链表的查找要遍历10个结点,而使用索引后,只需要遍历7个结点。可以看出,加了一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是说查找效率提高了。
如果我们在第一级索引的基础上,建第二级索引。现在再来查找16,需要遍历的结点数量(6)又减少了。
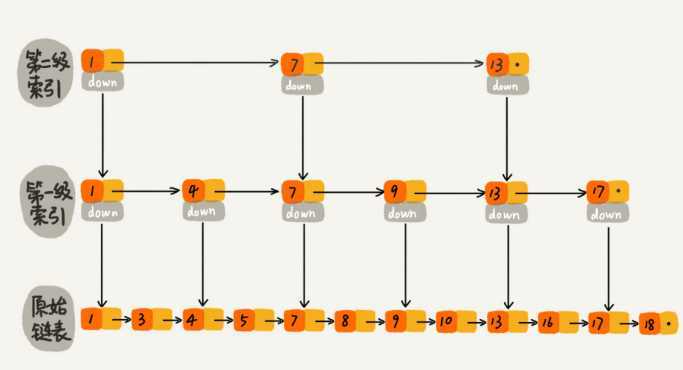
前面讲的这种链表加多级索引的结构,就是跳表。
跳表查询有多快
算法的执行效率可以时间复杂度来度量。我们知道,在一个单链表中查询某个数据的时间复杂度是O(n)。那在一个具有多级跳表中,查询某个数据的时间复杂度是多少呢?
假设链表里有n个结点。按照每两个结点抽出一个结点作为上一级的结点,那第一级索引的结点个数大约是n/2,第二级索引结点个数大约是n/4,以此类推,第k级索引的结点个数是第k-1级索引的结点个数的1/2,那么第k级索引结点个数是n/(2^k)。
假设索引有h级,最高级的索引有2个结点,通过上面的公式,可以得到n/(2^h)=2,从而求得h=log2(n-1)。如果包含原始链表这一层,整个跳表的高度就是log2(n)。
在跳表中查询某个数据的时候,如果每一层都要遍历m个结点,那跳表中查询一个数据的时间复杂度就是O(m*logn)。
按照前面这种索引结构(每两个结点抽出一个结点作为上一级的结点),每一级索引最多只需要遍历3个结点,即m=3。
假设要查找的数据是x,在第k级索引中,遍历到y结点之后,发现x>y,x<z,就通过y结点的down指针下降到第k-1级索引。在第k-1级索引中,y和z之间只有3个结点(包含y和z),以此类推,每一级索引都最多只需要遍历3个结点。
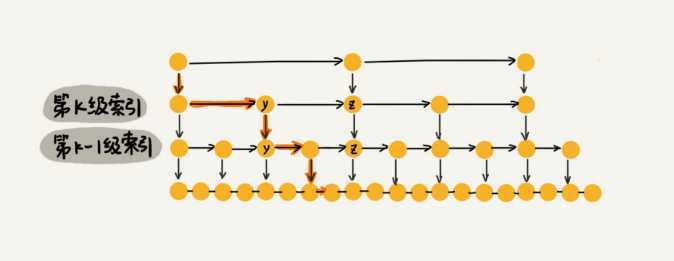
所以跳表中查询任意数据的时间复杂度是O(logn)。
跳表是不是很浪费内存
比起单链表,跳表要存储多级索引,相对要消耗更多的存储空间。
假设原始链表大小是n,那第一级索引大约是n/2,第二级索引大约是n/4,以此类推,直到第k层索引剩下2个结点。

这是一个等比数列,索引总和是n/2+n/4+n/8+....+8+4+2=n-2。所以跳表的空间复杂度是O(n)。
高效的动态插入和删除
我们知道,在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是O(1)。但定位位置这个查找操作就会比较耗时。
相对单链表的查找的时间复杂度O(n),跳表的查找的时间复杂度是O(logn)。
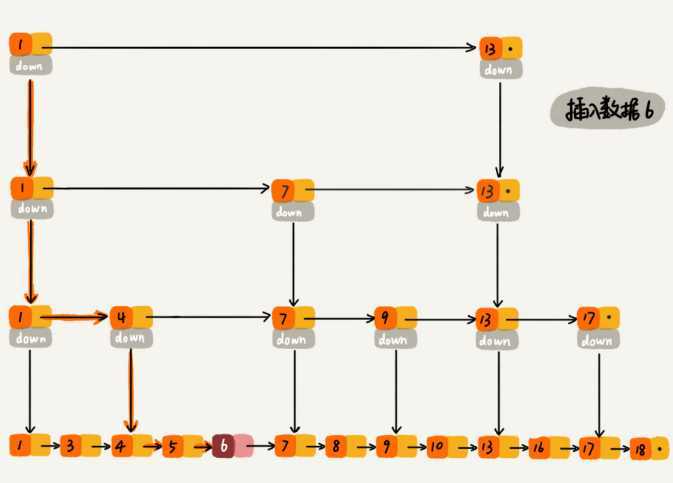
删除操作跟插入类似,但如果这个结点在索引中也有出现,那还要删除索引中的。
跳表索引动态更新
当不停往跳表中插入数据时,如果不更新索引,那可能出现某2个索引结点之间数据非常多的情况。极端情况下,跳表会退化成单链表。
可以通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值K,那就将这个结点添加到第一级到第K级这个K级索引中。
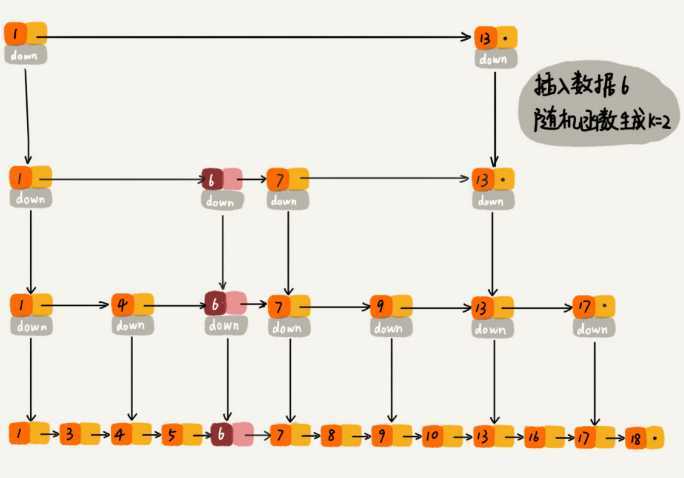
代码实现
public class AdvancedSkipList
{
/// <summary>
/// 最大索引层级
/// </summary>
private static readonly int MAX_LEVEL = 16;
/// <summary>
/// 索引层级
/// </summary>
private int levelCount = 1;
/**
* 带头链表
*/
private Node head = new Node(MAX_LEVEL);
private Random random = new Random();
public Node Find(int value)
{
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i)
{
while (p.forwards[i] != null && p.forwards[i].data < value)
{
// 找到前一节点
p = p.forwards[i];
}
}
// 0层表示原始数据层,判断是否查找的value
if (p.forwards[0] != null && p.forwards[0].data == value)
{
return p.forwards[0];
}
else
{
return null;
}
}
/**
* 插入方法
*/
public void Insert(int value)
{
int level = head.forwards[0] == null ? 1 : RandomLevel();
// 每次只增加一层,如果条件满足
if (level > levelCount)
{
level = ++levelCount;
}
Node newNode = new Node(level);
newNode.data = value;
//newNode.maxLevel = level;
Node[] update = new Node[level];
for (int i = 0; i < level; i++)
{
update[i] = head;
}
// 记录每个索引层小于value的最大值结点
Node p = head;
for (int i = level - 1; i >= 0; --i)
{
while (p.forwards[i] != null && p.forwards[i].data < value)
{
p = p.forwards[i];
}
// levelCount会 > level,所以加上判断
if (level > i)
{
update[i] = p; // use update save node in search path
}
}
// in search path node next node become new node forwords(next)
for (int i = 0; i < level; ++i)
{
newNode.forwards[i] = update[i].forwards[i];
update[i].forwards[i] = newNode;
}
//// update node hight
//if (levelCount < level) levelCount = level;
}
public void Insert2(int value)
{
int level = head.forwards[0] == null ? 1 : RandomLevel();
// 每次只增加一层,如果条件满足
if (level > levelCount)
{
level = ++levelCount;
}
Node newNode = new Node(level);
newNode.data = value;
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i)
{
while (p.forwards[i] != null && p.forwards[i].data < value)
{
// 找到前一节点
p = p.forwards[i];
}
// levelCount 会 > level,所以加上判断
if (level > i)
{
if (p.forwards[i] == null)
{
p.forwards[i] = newNode;
}
else
{
Node next = p.forwards[i];
p.forwards[i] = newNode;
newNode.forwards[i] = next;
}
}
}
}
/**
* 作者zheng的插入方法,未优化前,优化后参见上面insert()
*
* @param value
* @param level 0 表示随机层数,不为0,表示指定层数,指定层数
* 可以让每次打印结果不变动,这里是为了便于学习理解
*/
public void Insert(int value, int level) {
// 随机一个层数
if (level == 0) {
level = RandomLevel();
}
// 创建新节点
Node newNode = new Node(level);
newNode.data = value;
// 表示从最大层到低层,都要有节点数据
newNode.maxLevel = level;
// 记录要更新的层数,表示新节点要更新到哪几层
Node[] update = new Node[level];
for (int i = 0; i < level; ++i) {
update[i] = head;
}
/**
*
* 1,说明:层是从下到上的,这里最下层编号是0,最上层编号是15
* 2,这里没有从已有数据最大层(编号最大)开始找,(而是随机层的最大层)导致有些问题。
* 如果数据量为1亿,随机level=1 ,那么插入时间复杂度为O(n)
*/
Node p = head;
for (int i = level - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
// 这里update[i]表示当前层节点的前一节点,因为要找到前一节点,才好插入数据
update[i] = p;
}
// 将每一层节点和后面节点关联
for (int i = 0; i < level; ++i) {
// 记录当前层节点后面节点指针
newNode.forwards[i] = update[i].forwards[i];
// 前一个节点的指针,指向当前节点
update[i].forwards[i] = newNode;
}
// 更新层高
if (levelCount < level) levelCount = level;
}
public void Delete(int value)
{
Node[] update = new Node[levelCount];
Node p = head;
for (int i = levelCount - 1; i >= 0; --i)
{
while (p.forwards[i] != null && p.forwards[i].data < value)
{
p = p.forwards[i];
}
update[i] = p;
}
if (p.forwards[0] != null && p.forwards[0].data == value)
{
for (int i = levelCount - 1; i >= 0; --i)
{
if (update[i].forwards[i] != null && update[i].forwards[i].data == value)
{
update[i].forwards[i] = update[i].forwards[i].forwards[i];
}
}
}
//while (levelCount > 1 && head.forwards[levelCount] == null)
//{
// levelCount--;
//}
}
/**
* 随机 level 次,如果是奇数层数 +1,防止伪随机
*/
private int RandomLevel()
{
int level = 1;
for (int i = 1; i < MAX_LEVEL; ++i)
{
if (random.Next() % 2 == 1)
{
level++;
}
}
return level;
}
public void PrintAll()
{
Node p = head;
while (p.forwards[0] != null)
{
Console.Write(p.forwards[0] + " ");
p = p.forwards[0];
}
Console.WriteLine();
}
/**
* 打印所有数据
*/
public void PrintAll_Beautiful()
{
Node p = head;
Node[] c = p.forwards;
Node[] d = c;
int maxLevel = c.Length;
for (int i = maxLevel - 1; i >= 0; i--)
{
do
{
Console.Write((d[i] != null ? d[i].data.ToString() : null) + ":" + i + "-------");
} while (d[i] != null && (d = d[i].forwards)[i] != null);
Console.WriteLine();
d = c;
}
}
/**
* 跳表的节点,每个节点记录了当前节点数据和所在层数数据
**/
public class Node
{
public int data = -1;
/**
* 表示当前节点位置的下一个节点所有层的数据,从上层切换到下层,就是数组下标-1,
* forwards[3]表示当前节点在第三层的下一个节点。
**/
public Node[] forwards;
public int maxLevel = 0;
public Node(int level)
{
forwards = new Node[level];
}
public override string ToString()
{
StringBuilder builder = new StringBuilder();
builder.Append("{ data: ");
builder.Append(data);
builder.Append("; levels: ");
builder.Append(maxLevel);
builder.Append(" }");
return builder.ToString();
}
}
}
原文:https://www.cnblogs.com/liang24/p/13185899.html