题目:在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
1. 题目难度:四星
2. 考察点:数组,二分查找
3. 简要说明:这是一道对二维数组进行二分查找的算法,考察对二分查找的灵活运用。
方法1:暴力算法
1. 分析:直接遍历一遍数组,即可判断目标target是否存在。
2. 复杂度分析
时间复杂度:O(n^2),因为最坏情况下,数组中的元素都需要遍历一次。
空间复杂度:O(1)
3. 代码:
方法二:二分查找
1. 分析:对于方法一,此题有额外信息没有利用上,数组从左到右递增,从上到下递增。有序的数组很显然应该想到二分。那么应该如何二分呢?
回想一下一维有序数组查找某个值二分的过程,如下图所示:
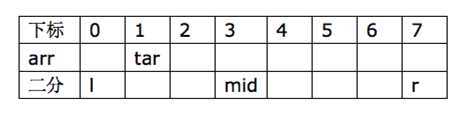
假设目标tar在arr[1]处,那么我们的二分过程就是:
1)设初始值:定义一个二分的开始下标为l,结束下标为r,如图所示:
2)二分一半,中间位置为 mid = l + ((r - l) >> 1), val>>1, 表示val右移一位相当于val/2,相当于 l+(r-l)/2,这样的写法是防止溢出。如果写成 mid = (l+r)/2; l+r可能会溢出。
3) 如果 tar == arr[mid],说明找到tar
4)比较:如果tar > arr[mid], 说明tar在区间[mid+1, r]中,l = mid + 1
5)如果tar < arr[mid],说明tar在区间[l, mid-1]中, r = mid - 1
图中的例子就是步骤 4)的情况,一次比较之后,如图所示,表示找到了tar。
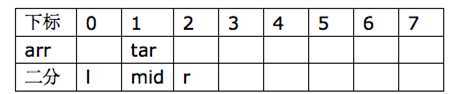
原文:https://www.cnblogs.com/lf6688/p/13181250.html