Python_DL_麦子学院（算法与应用_进阶）_10~

4.1 Backpropagation算法上

1）传统的分类器：

上一节，我们利用了3层神经网络算法，来识别数字，达到了95%的精确度。这里我们不以图片的像素点为输入，用神经网络算法，而以平均灰度作为衡量准确率的指标。

平均灰度（Average Darkness）：输入照片是由像素点组成的（28*28=784），每一个像素点都有一个灰度值是0~255，归一化后将这 个值降到了[0,1]。可以把所有像素点的灰度值相加，再除以784，得出来得值做为metrix去衡量。看训练集得每一个数字图片的值与测试集中每一个数字图片的值最相近，我们就把他识别为相应的数字。

SVM：正确率能达到94.3%

2） backpropagation算法的基础（标签方式及假定）

在1970年就被提出，1986年的David Rumelhart, Geoffrey Hinton, and Ronald Williams提出的论文才得到重视，可以解决神经网络中的学习。 

Backpropagation核心解决的问题：dC/dw 和 dC/db 的计算，针对cost函数C

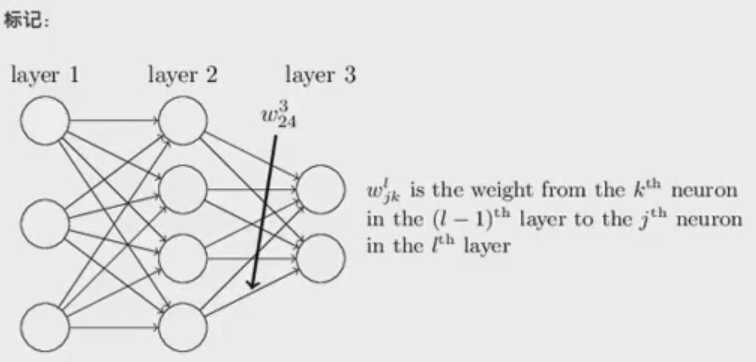
w的标记（神经元之间的连接）：第l-1层的第k个神经元到第l层的第j个神经元的权重。l表示第几层网络，j和k表示神经元。W³₂₄表示：第2层第4个神经元到第3层第2个神经元的权重。

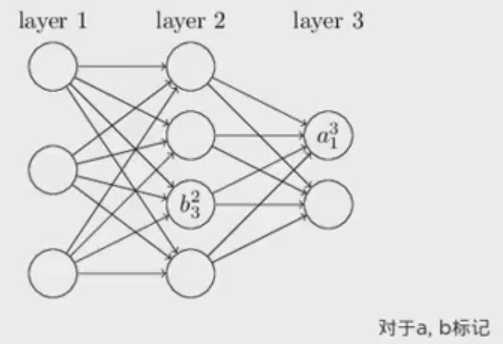
b表示bias是每个神经元的标记，b²₃表示第二层的第三个神经元。

a表示activation function，激活值。a³₁表示在第三层的第一个神经元。

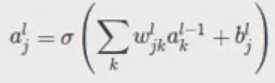
feedforward步骤：

1. 加权求和，Σwx+b。
2. 再用sigmoid函数对上一步的结果做激励。

对于每一层（l），定义一个weight matrix（权重矩阵）：w^l

连接l层和l-1层，矩阵中第j行，第k列的元素就是：w^l_jk

对于每一层（l），定义一个bias vector：b^l

表示当前层的每一个元素的bias是：b^l_j

同理，对于a：a^l_j 和 a^l

vectorizing a function: σ(v)_j = σ(v_j) ：表示对向量求方程等于对每个元素求方程：

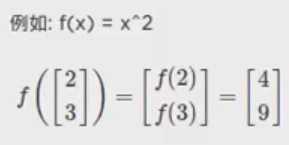
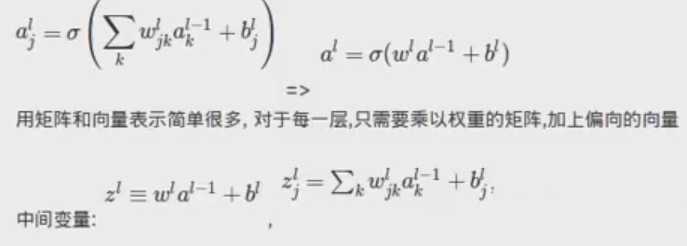
关于Cost函数的两个假设：

 L：表示神经网络的层数，说明Cost要每层都要计算。cost可以求全部的平均cost，也可以是求单个x的cost。

因为对于back propagation，dC/dw 和 dC/db 的计算是通过单个实验x完成的。

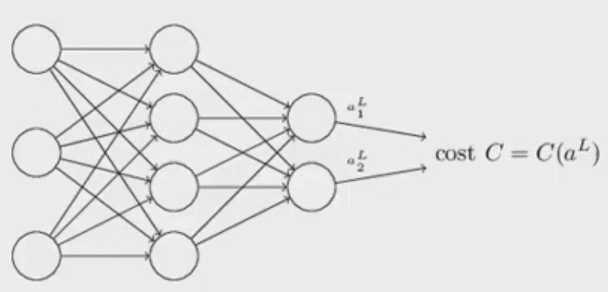
Cost可以被写成神经网络输入出的一个函数

我们定义的这个二次cost方程满足这点： 

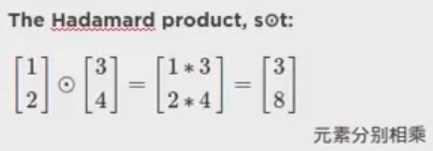
4.2 Back propagation算法中

1）Backpropagation的四个关键公式：

 定义error在第l层，第j个神经元：

Python_DL_麦子学院（算法与应用_进阶）_10~

原文：https://www.cnblogs.com/tlfox2006/p/13109893.html