关于Cohen-Sutherland 直线段裁剪算法思想概述
直线段裁剪是二维图形裁剪的基础,本质是判断直线段是否与窗口边界相交,如相交则进一步确定直线段上位于窗口内的部分。
算法思想:直线的端点赋予一组4位二进制码,成为RC(区域编码),裁剪窗口的四条边所在的直线可以把平面分为9个区域,对各个区域的编码也是四位,C3C2C1C0,分别代表上下右左四个窗口边界。裁剪窗口所在的区域为0000,对于直线段上的端点进行编码,等于该端点所在的区域的编码。

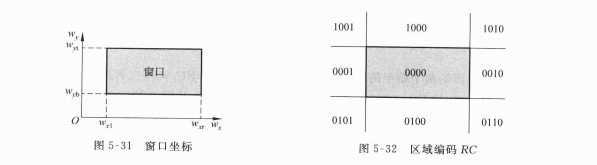
编码后就容易判断两个端点的情况:
比如两个端点求与不等于0,即RC0&RC1≠0;说明该线段在裁剪窗口之外,应简弃;
两个端点RC编码按位或为0,即RC0|RC1=0。说明直线段两个端点都在窗口内,应简取。
还有第三种情况:不满足前两种情况的,说明直线段与边界或其延长线有交点,要进行求交判断:
①此时直线段与边界相交,P0P1和两个边界相交,按左右下上的顺序计算交点,设交点为P,注意:总是要让直线段的一个顶点处于窗口之外,例如P0点。这样P0点到交点P的直线段必然不可见,故可以将交点外的线段简弃。
②直线段与边界的延长线相交,直线段在窗口外,也不在窗口同一侧。依旧按照左右下上顺序计算,将延长线与线段交点定为P,有PP0,位于窗口某侧,被简弃。
如果求裁剪后窗口内直线段的端点坐标,(那一般是求P1,以实际题目为准,看剪了哪部分),两点求直线方程,然后带入相交边界的x或y值可得。
[ 计算机图形学 ] 复习Cohen-Sutherland 直线段裁剪算法
原文:https://www.cnblogs.com/dabuliu/p/13092772.html