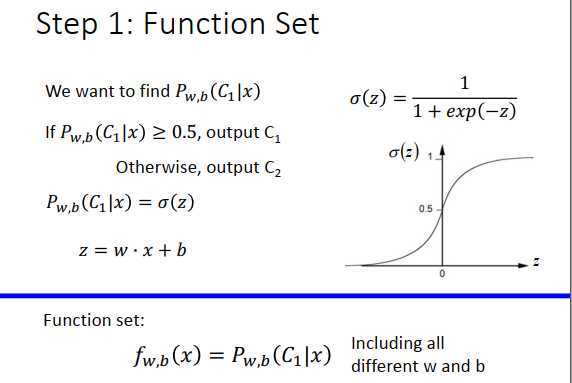
在logistic里,我们要找的是一个后验概率\(P_{w,b}(C_1|x)\)
\(P_{w,b}(C_1|x)\geq 0.5\),output \(C_1\)
\(P_{w,b}(C_1|x)\)<0.5,output \(C_2\)
后验概率由\(\sigma(z)\)计算,\(\large \sigma(z)=\frac{1}{1+exp(-z)}\),\(z=w \cdot x+b=\sum\limits_iw_ix_i+b\)。
\(w\) 是一个向量,每个维度用下标\(i\)表示。
函数集表示为\(\large f_{w,b}(x)=P_{w,b}(C_1|x)\),受\(w,b\)控制。
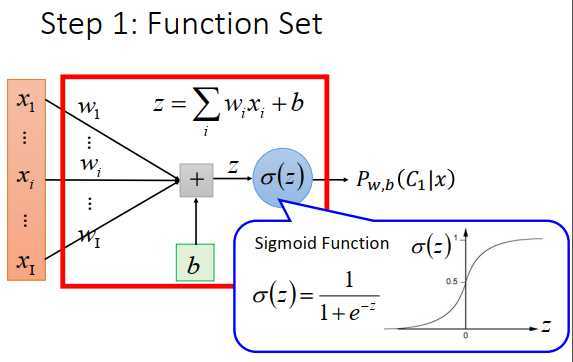
函数里有两组参数,\(w\)称为权重,\(b\)称为偏置。
input是\(x_1\)到\(x_I\),乘上\(w_1\)到\(w_I\),再加上b,得到\(z\),\(\sigma(z)\)的图像如上图右下。

logistic 回归和线性回归做一下比较

假设有N笔训练数据,每笔数据要有label。
假设这些数据是从函数\(f_{w,b}(x)\)定义的后验概率中产生的。
给定一组参数\(w,b\) ,就决定了这个后验概率,然后可以计算产生这N笔数据的概率。
产生这N笔数据的概率怎么算?
其他数据都依次计算概率,定义\(L(w,b)\)是所有数据的概率乘积,也叫似然函数。
\(w^*,b^*\)是一组可以最大化\(L(w,b)\)的参数。
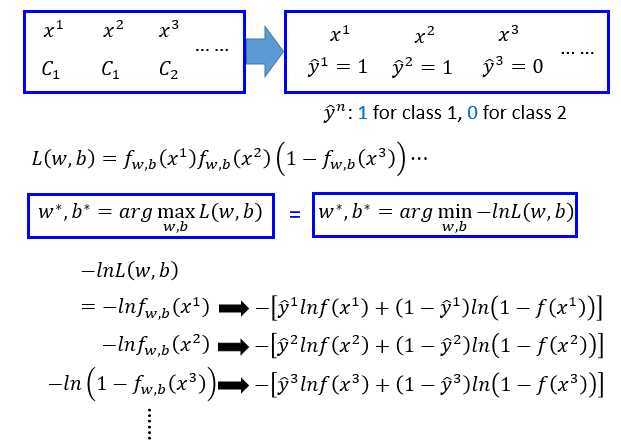
做一个数学上转换
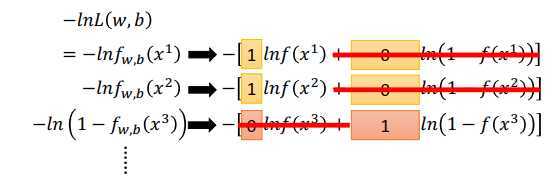
最大化似然函数\(L(w,b)\)等同于最小化负对数似然函数\(-lnL(w,b)\)(取ln不影响大小顺序,乘积取ln变成加法运算,计算简单一点)。如上图最下面所示,由于\(x\)可以属于两个类,1和0,那么\(\large f_{w,b}(x)\)表示属于1的概率,\(\large 1-f_{w,b}(x)\)则表示属于0的概率。
那么\(\large ln f_{w,b}(x)\)可改写为 \(\large \hat y ln f_{w,b}(x)+(1-\hat y)ln(1-f_{w,b}(x))\)

根据上面的改写公式,负对数似然函数可改写为
\(\large -lnL(w,b)=\sum\limits_n-[\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f_{w,b}(x^n))]\),等式右边是伯努利分布的交叉熵。
为什么叫做交叉熵,和信息论也没有直接的关系?
假设有两个分布 \(\large p,q\) 如上图最下方所示,那么\(\large p,q\)之间的交叉熵为\(\large H(p,q)=-\sum\limits_xp(x)ln(q(x))\),对\(x\)求和后的公式和上面的公式一致。
交叉熵的含义是两个分布有对接近,越大差别越大,如果是一模一样的分布,交叉熵就为0。

怎么定义一个函数的好坏?
如果有训练数据,class 1标注为1,class 2 标注为0,把函数的output和target都看作是伯努利分布的话,希望两个分布越接近越好,那么损失函数为伯努利分布\(f(x)\)和伯努利分布\(\hat y\)的交叉熵,最小化交叉熵优化参数。

使用梯度下降求解参数,对\(w_i\)微分。\(\sigma(z)\)对\(z\)的微分为\(\sigma(z)(1-\sigma(z))\),可以背下来。
上图右下方是\(\sigma(z)\)和微分的图像,在头和尾的地方\(\sigma(z)\)的斜率接近于0,在中间最大。
注意这里的\(x_i^n\)意思是第\(n\)个样本的第\(i\)个特征

右边项对\(w_i\)偏微分

最后得到的微分结果,并更新\(w_i\)。
\(w_i\)的更新取决于三件事:

逻辑回归和线性回归的梯度更新公式是一样的,不同点在于


假如用Square Error做为损失函数,那么\(\large L(f)=\frac{1}{2}\sum\limits_n(f_{w,b}(x^n)-\hat{y}^n)^2\),仍然使用梯度下降求解参数。对\(w_i\)偏微分得到的式子为\(\large 2(f_{w,b}(x)-\hat y)f_{w,b}(x)(1-f_{w,b}(x))x_i\),用这个式子更新参数会有问题。
当第n个样本的\(\hat{y}^n=1\)时:
当第n个样本的\(\hat{y}^n=0\)时:
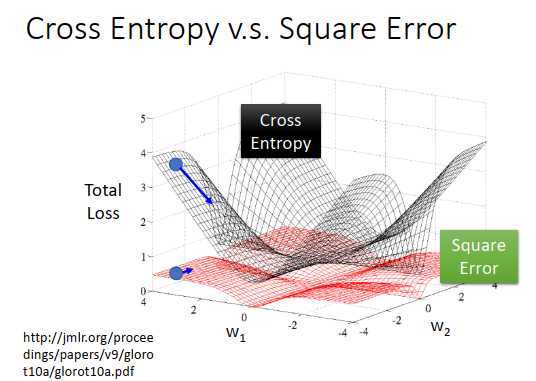
上图是参数的变化对total loss作图,黑色的是交叉熵,红色的是均方误差
假设两个损失超平面的中心点是我们的目标点,那么此处的微分很小。
如果是交叉熵的损失平面,会发现离目标点越远,微分值越大,那么参数更新速度越快,幅度越大,这个没有问题。
但是选择均方误差的话,会发现距离目标点很远时,微分却非常小,说明参数移动速度很慢,如果随机找一个参数的初始值,一开始就卡住不更新了,就算此时想调整学习率(离目标近设小一点,离目标远设大一点),也不清楚到底是在目标点附近还是在很远的地方(目标点附近的微分也非常小)

Logistic回归的方法称之为判别式方法,用高斯生成后验概率的方法称之为生成式模型。事实上,在做概率模型时,把高斯模型的协方差设置为共享协方差的话,两个方法的model、function set是一样的,都是\(\sigma(w\cdot x+b)\),找不同的\(w,b\)就可以得到不同的函数。
用Logistic回归可以用梯度下降法直接找出\(w,b\)。
用高斯模型的话,首先会计算\(\mu_1,\mu_2\)和\(\Sigma^{-1}\),再根据\(\mu_1,\mu_2,\Sigma^{-1}\)计算\(w,b\) 如上图右下方
上图左边和右边找出来的\(w,b\)会是同一组吗?
其实是不同的,虽然使用的是同样的函数集,但是因为作了不同的假设,导致根据同一组训练集训练出来的参数不同。
Logistic回归对后验概率没有分布假设(但是对target是有假设的,即假设target服从伯努利分布,出现负的概率为1-p,当后验概率>1-p时,判断为正),单纯去求解\(w,b\)
但是在生成式模型中,对后验概率是有假设的,比如假设服从高斯分布、伯努利分布、朴素贝叶斯等等,根据这些假设找到另外一组\(w,b\)
这两组\(w,b\)不会是同一组
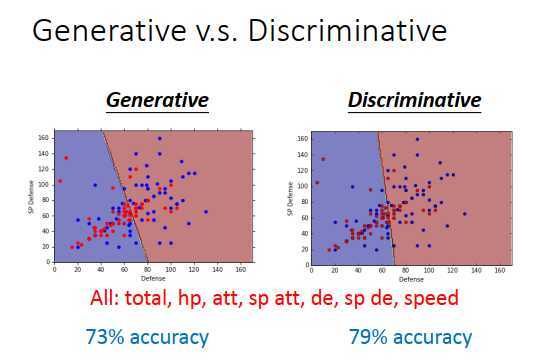
哪一组的\(w,b\)比较好?
如上图,蓝色点是水性宝可梦,红色点是一般的宝可梦。特征只有defense时,生成式模型和判别式模型的边界如上图所示,从这个结果很难看出谁更好。
然后使用7个特征,生成式模型的准确率为73%,判别式模型的准确率为79%,很多文献上,有说判别式模型的效果会比生成式模型的好。

为什么判别式模型的效果会比生成式模型的好?
假设有一笔训练数据,总共13个样本,每个样本有两个特征,1个样本为class1,其余12个样本为class2,特征取值如上图最上方所示。
现在给一个测试样本,特征都为1,如上图,从人类角度学习,判断为哪一类?一般都觉得是第一类。
从朴素贝叶斯角度,第一个特征为1从某个class产生的概率为\(P(x_1|C_i)\),第二个特征为1从某个class产生的概率为\(P(x_2|C_i)\),那么从某个class产生这个样本的概率为\(P(x|C_i)=P(x_1|C_i) P(x_2|C_i)\)。
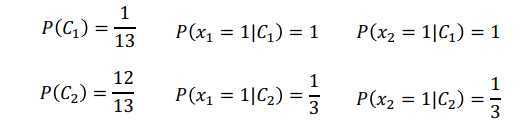
计算先验概率和类条件概率

估测一个测试数据来自class 1的概率
\(P(x|C_1)=P(x_1|C_1)P(x_2|C_1)=1 \times 1\)
\(P(x|C_2)=P(x_1|C_2)P(x_2|C_2)=\frac{1}{3} \times \frac{1}{3}\)
\(P(x)=\sum\limits_i P(x,C_i)=P(x,C_1)+P(x,C_2)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2)\)
实际做运算,发现\(P(C_1|x)\)<0.5,那朴素贝叶斯认为这笔数据是来自class 2的,和人类的直觉相反。
你会觉得测试数据里,两个特征都为1,那应该是来自于class 1 才对。可是对朴素贝叶斯来说,它不考虑不同维度之间的关系,对它来说,两个维度是独立产生的,在训练数据里之所以没有这样的数据,是因为样本不够多。
所以生成式模型和判别式模型的区别在于,生成式模型做了一些假设,相当于脑补了一些事情,在训练数据里明明没有观察到特征都是1的数据,朴素贝叶斯还是想象自己看到了。

那脑补是一件好的事吗?
通常来说不是一件好的事情,因为数据没有告诉你。但是在数据很少的情况下,脑补有时候也会有用。
有时候判别式模型不一样比生成式模型好
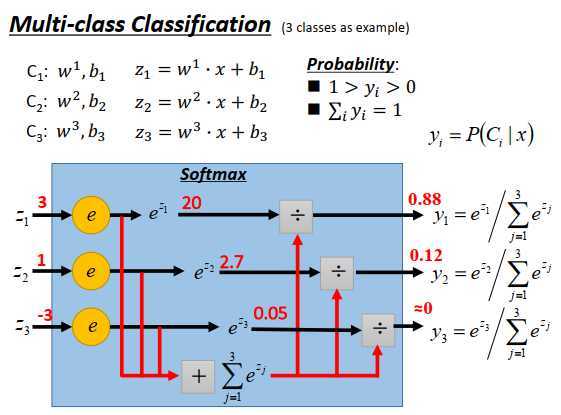
原理和二分类几乎是一模一样的。
现在有三个class \(C_1,C_2,C_3\),每一个class 都有一组自己的权重和偏置,\(w_1,w_2,w_3\)代表三个向量,\(b_1,b_2,b_3\)代表三个标量,然后input一个\(x\),计算\(z_1,z_2,z_3\)如上图所示,\(z_1,z_2,z_3\)可以是任何实数(负无穷到正无穷),接下来把\(z_1,z_2,z_3\)丢进softmax函数。
softmax函数的一个例子:
经过softmax之后,output被限制在0到1(一定是正的),\(y_i\)和一定为1,因为处以total sum相当于做了一个规范化。
为什么叫做softmax?
max是取最大值,softmax的意思是对最大值做强化,因为取了exp,大的值和小的值之间的差距会被拉得更开。
softmax的output \(y_i\)则是第\(i\)个class的后验概率,例如属于class 1的概率是88%,属于class 2的概率是12%,属于class 3 的概率趋近于0。
为什么取exp,output 为后验概率?
Bishop的教科书,P209-210
如果今天又3个class,3个class都是高斯分布,共享一个协方差矩阵,做一般推导后就是softmax函数。也可以从最大熵原理推出softmax。
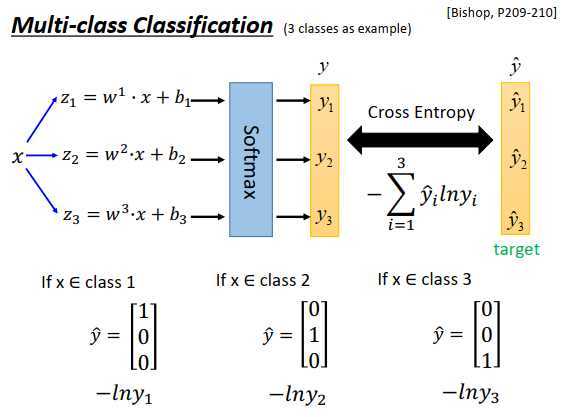
一个input x,分别乘上3组不同的群众,加上3组不同的偏置,得到3个不同的\(z\) ,通过softmax函数得到 \(\large y_1,y_2,y_3\) 3个类别的后验概率,计算和target \(\large \hat{y_1},\hat{y_2},\hat{y_3}\)的交叉熵\(\large -\sum\limits_{i=1}^3 \hat{y_i}ln (y_i)\)。
要计算交叉熵,那么\(\large \hat y\)也要是一个概率分布:
之前讲过假设class 1=1,class2=2,class3=3会有问题,因为假设了1跟2比较近,2跟3比较近,这样会有问题。但是使用上述向量形式,就没有假设谁跟谁比较近的问题。
交叉熵的式子怎么来的?
也是从最大化似然函数推导出来的。
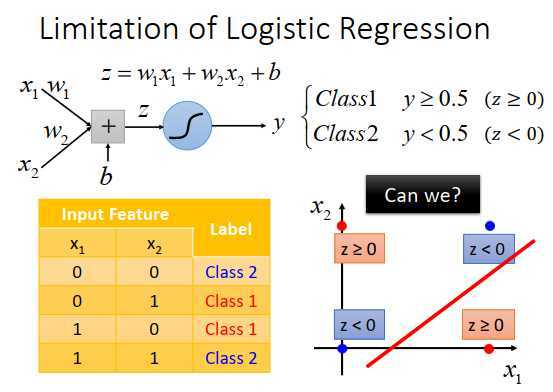
假设现在有4个数据,有两个伯努利特征,把他们画出来是上图右下所示。现在使用logistic回归无法对他们进行正确分类。在logistic回归中,希望两个属于class 1的红色点的概率$\geq $0.5,属于class 2的蓝色点的概率<0.5。
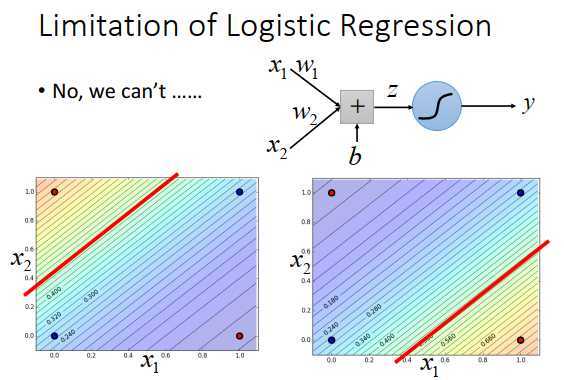
因为logistic回归在两个class之间的边界就是一条直线,在feature的平面上只能画一条直线,画出的2种情况如上图最下方所示。不管怎么画,都无法完全区分红色点和蓝色点(可以随便画直线)。
如果坚持用logistic 回归,怎么办?
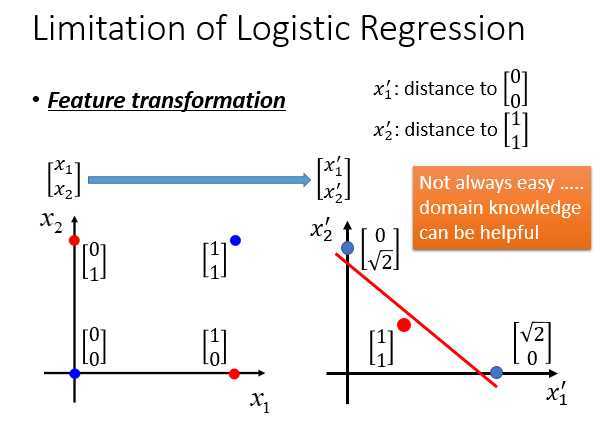
有一招叫做Feature Transformation,原来\(x_1,x_2\) 特征定的不好,可以做转化找一个比较好的feature space,可以让logistic回归进行处理。
把\(x_1,x_2\)转到另一个space \(x_1‘,x_2‘\)上(怎么做特征转换是很启发式和临时性的东西,例如用自己喜欢的方式)。例如定义\(x_1‘\)就是某个点到(0,0)的距离,\(x_2‘\)是某个点到(1,1)的距离。
例如左下角的红色点\(\begin{bmatrix} 0\\0 \end{bmatrix}\),跟\(\begin{bmatrix} 0\\0 \end{bmatrix}\)的距离为0,跟\(\begin{bmatrix} 1\\1 \end{bmatrix}\)的距离为\(\sqrt{2}\)。
变换后的数据,对logistic来说可以处理了,麻烦的问题是我们不知道怎么做特征转换是好的,花太多力气做特征转换,就不是机器学习,而是人工智慧了。所以我们会希望让机器自己产生好的transformation。
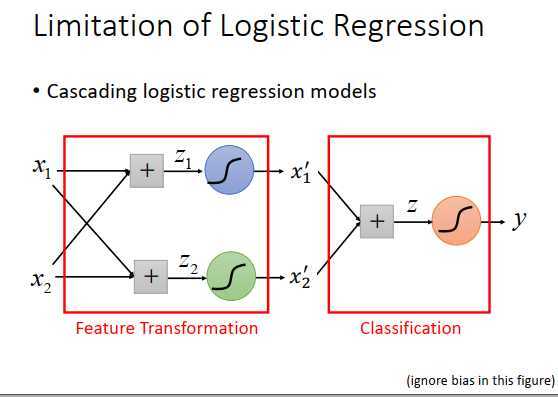
怎么让机器自己产生好的transformation?
把多个logistic回归级联起来,假设input是\(x_1,x_2\) ,把偏置忽略掉,分别乘以权重相加得到\(z_1,z_2\) ,通过两个sigmoid函数得到output \(x_1‘,x_2‘\) ,就是新的经过transform之后的特征,在这两个特征平面上,class1和class2可以被一条直线分开,那么只要在\(x_1‘,x_2‘\) 后面再接一个logistic回归的model。
前面两个logistic回归做的事情就是特征转换,再由最后一个logistic回归做分类。
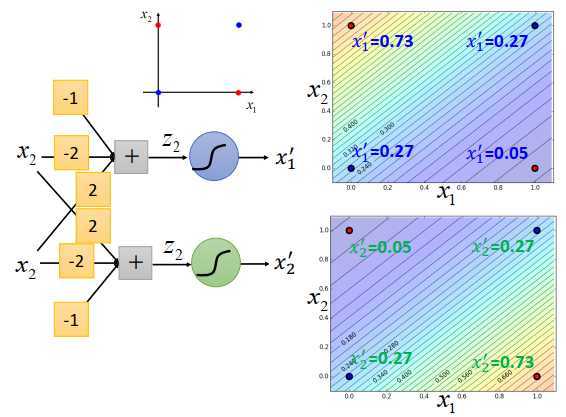
看之前的例子,在\(x_1,x_2\)平面上有4个点,
可以调整蓝色logistic回归的权重和偏置,让它的后验概率的output \(x_1‘\) 颜色像上图右上方一样,因为边界是一条直线,所以output的等高线是直线,颜色代表了等高线大小。左上角的地方,output比较大,右下角的地方,output比较小,此时4个点的\(x_1‘\)值为0.73,0.27,0.27,0.05,这件事情是可以做到的。
对绿色logistic回归函数来说,也可以调整权重和偏置,让4个点的\(x_2‘\)值为0.05,0.27,0.27,0.73,logistic回归的边界一定是一条直线,可以有任何的画法,可以左上高,右下低,也可以是右下高,左上低,只要调整参数都是可以做到的。
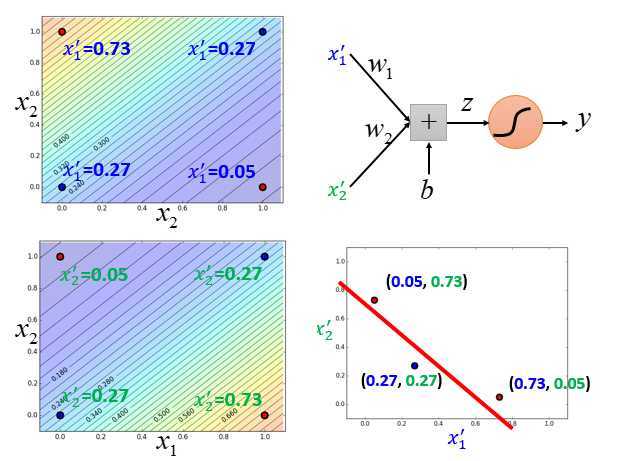
有了前面两个logistic回归之后,就可以把input的每一笔数据做特征转换得到另一组特征\(x_1‘,x_2‘\) 。
例如左上角这个点,原来在\(x_1,x_2\)平面上的坐标为(0,1),在\(x_1‘,x_2‘\)平面上的坐标为(0.73,0.05)。
右下角红色在\(x_1‘,x_2‘\)平面上的坐标为(0.05,0.73)。
做了转换后,再用上图右上方红色的logistic回归画一条边界,把蓝色的点和红色的点分开。
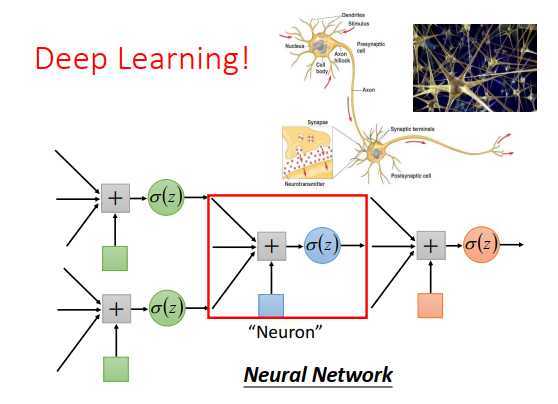
一个logistic回归的input来自于其他logistic回归的output。
一个logistic回归的output也可以是其他logistic回归的input。
我们可以给每个logistic回归一个新名称,叫做神经元,把这些logistic回归串起来的网络就是神经网络。
原文:https://www.cnblogs.com/wry789/p/13093688.html