贪心算法
特征:
def minCoins(V): available = [1, 2, 5, 10, 20, 50, 100, 500, 1000] result = [] for i in available[::-1]: while (V >= i): V -= i result.append(i) return result
二、活动问题
N个活动,每个活动的开始时间为si,结束时间是fi。如果 si ≥ fj or sj ≥ fidef printMaxActivities(acts): n = len(acts) sort_acts = sorted(acts, key=lambda tup: tup[1]) prev = sort_acts[0] print(prev) for curr in sort_acts: if curr[0] >= prev[1]: print(curr) prev = curr
三、最小的数字问题
def findSmallest(m, s): if (s == 0): if(m == 1) : print("Smallest number is 0") else : print("Not possible") return # 9999 if (s > 9 * m): print("Not possible") return res = [0 for i in range(m + 1)] # deduct sum by one to account for cases later # (There must be 1 left for the most significant digit) s -= 1 for i in range(m-1,0,-1): # If sum is still greater than 9, digit must be 9. if (s > 9): res[i] = 9 s -= 9 else: res[i] = s s = 0 res[0] = s + 1 print("Smallest number is ",end="") for i in range(m): print(res[i],end="")
四、两个数字的最小和
import heapq def minSum(a): heapq.heapify(a) num1 = 0 num2 = 0 while a: num1 = num1 * 10 + heapq.heappop(a) if a: num2 = num2 * 10 + heapq.heappop(a) return num1 + num2
五、以最低的成本连接绳索
import heapq def ropeCost(ropes): heapq.heapify(ropes) total = 0 while ropes: first = heapq.heappop(ropes) second = heapq.heappop(ropes) local = first + second total += local if not ropes: break heapq.heappush(ropes, local) return total
六:最小平台数
根据所有到达火车站的列车的到达和离开时间,找到火车站所需的最少数量的平台,以免def findPlatform(arr, dep, n): arr.sort() dep.sort() # plat_needed indicates number of platforms needed at a time plat_needed = 0 result = 0 i = 0 j = 0 # Similar to merge in merge sort to process all events in sorted order while (i < n and j < n): if (arr[i] < dep[j]): plat_needed += 1 i += 1 result = max(result, plat_needed) else: plat_needed -= 1 j += 1 return result
七、部分背包问题
def fracKnapsack(capacity, weights, values): numItems = len(values) valuePerWeight = sorted([[v / w, w, v] for v,w in zip(values,weights)], reverse=True) print(valuePerWeight) totalCost = 0. for tup in valuePerWeight: if capacity >= tup[1]: capacity -= tup[1] totalCost += tup[2] else: totalCost += capacity * tup[0] break return totalCost
八、将板子切割成正方形的最小成本
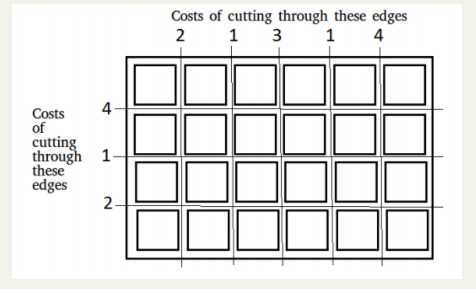
def minimumCostOfBreaking(X, Y, m, n): res = 0 # sort the horizontal cost in reverse order X.sort(reverse = True) # sort the vertical cost in reverse order Y.sort(reverse = True) # initialize current width as 1 hzntl = 1; vert = 1 # loop untill one or both # cost array are processed i = 0; j = 0 while (i < m and j < n): if (X[i] > Y[j]): res += X[i] * vert # increase current horizontal # part count by 1 hzntl += 1 i += 1 else: res += Y[j] * hzntl # increase current vertical # part count by 1 vert += 1 j += 1 # loop for horizontal array, if remains total = 0 while (i < m): total += X[i] i += 1 res += total * vert #loop for vertical array, if remains total = 0 while (j < n): total += Y[j] j += 1 res += total * hzntl return res
九、字典中最小的数组
def minimizeWithKSwaps(arr, n, k): for i in range(n-1): pos = i for j in range(i+1, n): # If we exceed the Max swaps then terminate the loop if ( j - i > k): break # Find the minimum value from i+1 to max (k or n) if (arr[j] < arr[pos]): pos = j # Swap the elements from Minimum position we found till now to the i index for j in range(pos, i, -1): arr[j],arr[j-1] = arr[j-1], arr[j] # Set the final value after swapping pos-i elements k -= pos - i
原文:https://www.cnblogs.com/oldby/p/13091715.html