洛谷 P1379 八数码难题 (BFS)

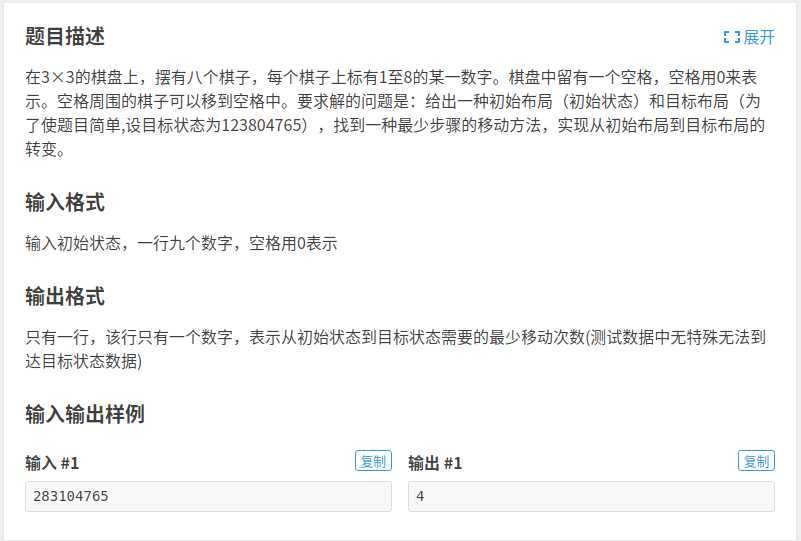
• 题意:有一个\(3\)x\(3\)的的棋盘,有八个\(1\)~\(8\)的棋子,每次可以将一枚棋子移动到四周的空位,问最少移动多少次,使得最后的状态为\(123804765\).

• 题解:直接BFS,用map来Hash存步数,这儿有个比较难想的点,就是把一维的坐标转化为二维的坐标(代码中有注释),然后我们找到\(0\)的位置,将四周可能的情况入队,不断下一层去找即可.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  const int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
  string s;
  
  int bfs(string s){
      string end="123804765";
      queue<string> q;
      unordered_map<string,int> dis;
      q.push(s);
      dis[s]=0;
  
      while(!q.empty()){
          auto tmp=q.front();
          q.pop();
  
          int d=dis[tmp];
          if(tmp==end) return d;
  
          int pos=tmp.find(‘0‘);
          int x=pos/3;      // dim 2
          int y=pos%3;
          for(int i=0;i<4;++i){
              int a=x+dx[i];
              int b=y+dy[i];
              if(a>=0 && a<3 && b>=0 && b<3){
                  swap(tmp[pos],tmp[a*3+b]);   //dim 1
                  if(!dis.count(tmp)){
                      dis[tmp]=d+1;
                      q.push(tmp);
                  }
                  swap(tmp[pos],tmp[a*3+b]);
              }
          }
      }
    return -1;
  }
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
      cin>>s;
      cout<<bfs(s)<<endl;
  
      return 0;
  }
  

洛谷 P1379 八数码难题 (BFS)

原文：https://www.cnblogs.com/lr599909928/p/13071835.html