微积分:
倒数和偏导数的定义与计算方法
导数定义:一元导数及函数斜率,反映因变量随自变量变化的快慢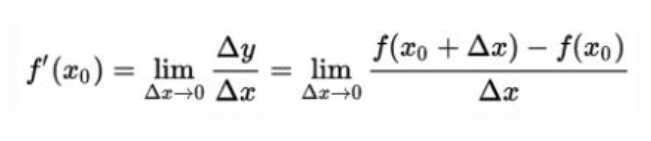
偏导数:偏导数对应多元函数的情况,对于一个 n元函数 y=f(x1,x2,…,xn),在 ?n 空间内的直角坐标系中,函数沿着某一条坐标轴方向的导数,就是偏导数
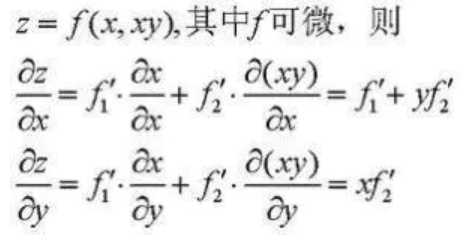
方向导数:函数在任意方向上的导数就是方向导数。

当α=0,方向I与梯度相同,增长最快;
当α=π,方向I与梯度相反,减少最快;
当α=π/2,方向I与梯度垂直,增长率为0;

全微分:
若函数z = f (x, y)在点(x, y)可微分,则该函数在点(x,y)的偏导数必存在,且函数z = f (x, y)在点(x,y)的全微分为
![]()
链式求导法则:
设u=u(x)、v=v(x)在x可导,z=f(u,v)在相应点(u,v)有连续偏导数,则复合函数z=f(u(x),v(x))在x可导,则有:
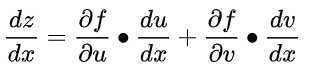
梯度向量的定义
极值定理
雅克比矩阵
Hession矩阵
凸函数的定义与判断方法
泰勒展开式
拉格朗日乘数法
原文:https://www.cnblogs.com/feichangnice/p/13047478.html