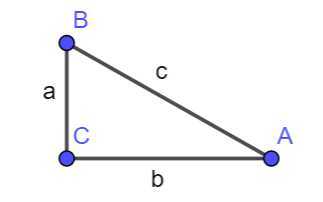
正弦: \(\sin A = \frac{a}{c} = \frac{对边}{斜边}\)
余弦: \(\cos A = \frac{b}{c} = \frac{邻边}{斜边}\)
正切: \(\tan A = \frac{a}{b} = \frac{对边}{邻边}\)
余切: \(\cot A = \frac{b}{a} = \frac{邻边}{对边}\)
特殊性质: |\(\sin \alpha\)| \(\leq 1\) , |\(\cos \alpha\)| \(\leq 1\)
| \(0°\) | \(15°\) | \(30°\) | \(45°\) | \(60°\) | \(75°\) | \(90°\) | |
|---|---|---|---|---|---|---|---|
| \(\sin\) | \(0\) | \(\frac{\sqrt{6}-\sqrt{2}}{4}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{6}+\sqrt{2}}{4}\) | \(1\) |
| \(\cos\) | \(0\) | \(\frac{\sqrt{6}+\sqrt{2}}{4}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{6}-\sqrt{2}}{4}\) | \(0\) |
| \(\tan\) | \(0\) | \(2-\sqrt{3}\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | \(2+\sqrt{3}\) | / |
| \(\cot\) | / | \(2+\sqrt{3}\) | \(\sqrt{3}\) | \(1\) | \(\frac{\sqrt{3}}{3}\) | \(2-\sqrt{3}\) | \(0\) |
若 \(\angle A + \angle B = 90°\) ,则 \(\sin A = \cos B\) , \(\tan A = \cot B\)
\(\tan A \cdot \cot A = 1\)
\(\tan A = \frac{\sin A}{\cos A}\)
\(\sin^2 A + \cos^2 A = 1\)
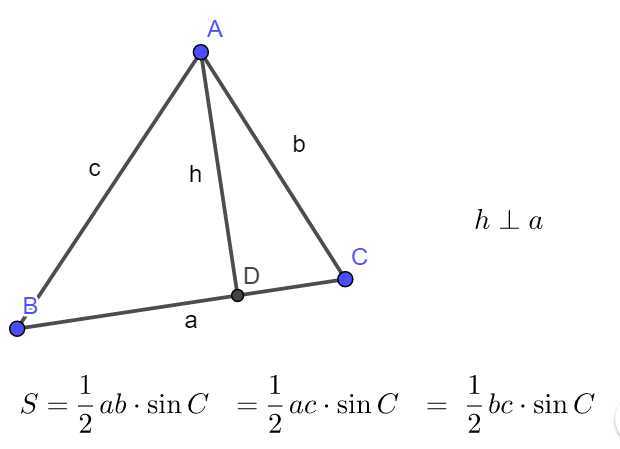
\(\sin (\alpha \pm \beta) = \sin \alpha \cdot \cos \beta \pm \sin \beta \cdot \cos \alpha\)
\(\cos (\alpha \pm \beta) = \cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta\)
\(\tan (\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \cdot \tan \beta}\)
六、倍角公式
\(\sin 2 \alpha = 2 \sin \alpha \cdot \cos \alpha\)
\(\cos 2 \alpha = \cos^2 \alpha - sin^2 \alpha = 1-2\sin^2 \alpha = 2\cos^2 \alpha -1\)
\(\tan 2 \alpha = \frac{2\tan \alpha}{1-\tan^2 \alpha}\)
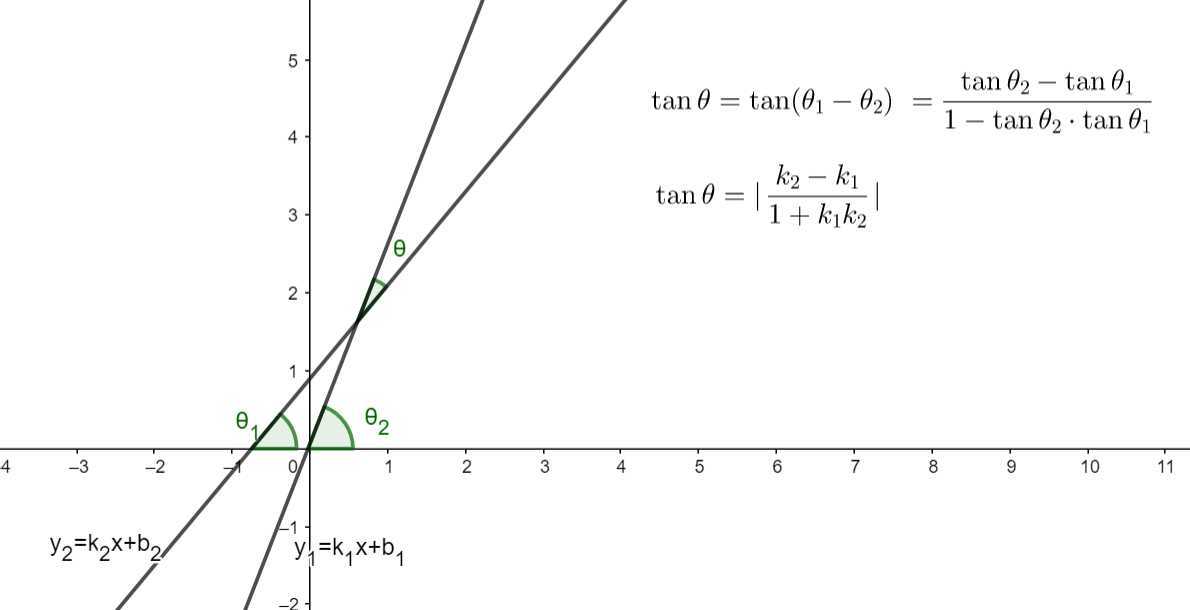
七、直线斜率
|\(k\)| \(= \tan \theta\) , \(\theta\) 为该直线与 \(x\) 轴相交所形成的最小夹角
原文:https://www.cnblogs.com/Ax-Dea/p/12996543.html