题目描述

题解

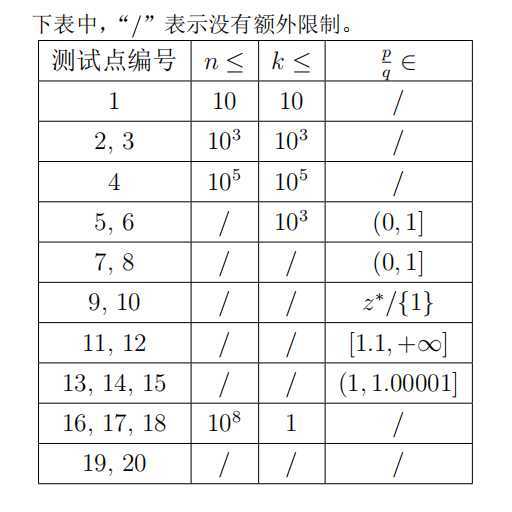
显然（并不）的结论：每一步肯定是能往后放就往后放

当p/q<=1时直接求自然数幂和即可，拉格朗日+线性筛预处理i^k

当p/q>1时总长不超√n，每次二分最后能放至少能加1的位置，然后再二分加的数

感受一下发现总轮数是logn的，假设当前位+1会增加k，那么n会变成n%k，至少减半

那么时间复杂度就i是√n*log^2（一个轮数一个二分）

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 1000000007
#define Mod 1000000005
#define ll long long
#define file
using namespace std;

ll w[1000003],Jc[1000003],a[50001],s,s2,ans,S1[1000004],S2[1000004],f[1000004],len,P[1000004];
int T,n,m,K,q,i,j,k,l,r,mid,I;
bool bz[1000004];
double p;

ll qpower(ll a,int b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}
bool check(int t,int s,bool tp)
{
	ll S,sum=n-s;
	int i;
	
	S=a[t]+s;
	if (tp) a[t]=S;
	fd(i,t-1,1)
	{
		sum-=ceil(S*p)-a[i];
		S=ceil(S*p);
		
		if (tp) a[i]=S;
		if (sum<0) return 0;
	}
	if (tp) n=sum;
	return sum>=0;
}

void init()
{
	int i,j,k,l;
	
	len=0;f[1]=1;
	fo(i,2,K+2)
	{
		if (!bz[i]) f[i]=qpower(i,K),P[++len]=i;
		
		fo(j,1,len)
		if (i*P[j]<=K+2)
		{
			f[i*P[j]]=f[i]*f[P[j]];
			if (!(i%P[j])) break;
		}
		else
		break;
	}
	memset(bz,0,1*(K+3));
}

int main()
{
	freopen("sequence.in","r",stdin);
	#ifdef file
	freopen("sequence.out","w",stdout);
	#endif
	
	w[1]=Jc[0]=Jc[1]=1;
	fo(i,2,1000002) w[i]=(mod-w[mod%i]*(mod/i))%mod,Jc[i]=Jc[i-1]*w[i]%mod;
	
	scanf("%d",&T);
	for (;T;--T)
	{
		scanf("%d%d%lf%d",&n,&K,&p,&q);ans=m=0;
		if (p<=q)
		{
			if (n<=K+2) {fo(i,1,n) ans=(ans+qpower(i,K))%mod;}
			else
			{
				S1[0]=S2[K+3]=1;s2=0;
				fo(i,1,K+2) S1[i]=S1[i-1]*(n-i)%mod;
				fd(i,K+2,1) S2[i]=S2[i+1]*(n-i)%mod;
				init();
				fo(i,1,K+2) s2=(s2+f[i])%mod,ans=(ans+s2*S1[i-1]%mod*S2[i+1]%mod*Jc[i-1]%mod*Jc[K+2-i]*((K+2-i)&1?-1:1))%mod;
			}
		}
		else
		{
			p/=q;
			r=floor(sqrt(n*2));
			while (n)
			{
				l=1;
				while (l<r)
				{
					mid=(l+r)/2;
					if (check(mid,1,0)) l=mid+1; else r=mid;
				}
				l-=!check(l,1,0);I=l;m=(!m)?I:m;
				
				l=1;r=floor(sqrt(n*2));
				while (l<r)
				{
					mid=(l+r)/2;
					if (check(I,mid,0)) l=mid+1; else r=mid;
				}
				l-=!check(I,l,0);check(I,l,1);
				
				r=I-1;
			}
			fo(i,1,m) ans=(ans+qpower(i,K)*a[i])%mod;
			memset(a,0,(m+1)*8);
		}
		printf("%lld\n",(ans+mod)%mod);
	}
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}

6641. 【GDOI20205.20模拟】sequence

原文：https://www.cnblogs.com/gmh77/p/12967256.html