【面试考】【入门】决策树算法ID3，C4.5和CART

关于决策树的purity的计算方法可以参考：
决策树purity/基尼系数/信息增益 Decision Trees
如果有不懂得可以私信我，我给你讲。

ID3

用下面的例子来理解这个算法：

下图为我们的训练集。总共有14个训练样本，每个样本中有4个关于天气的属性，这些属性都是标称值。输出结果只有2个类别，玩(yes)或者不玩(no)：

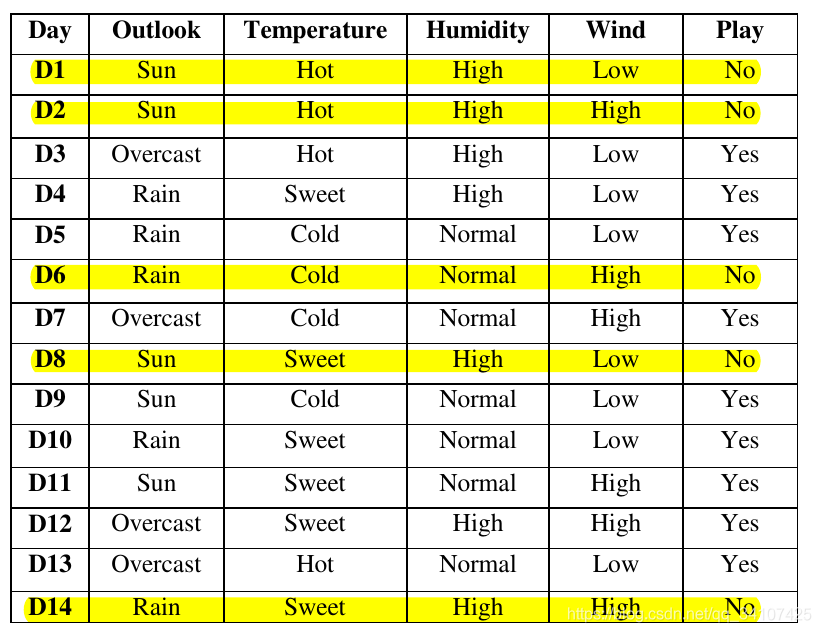
首先先计算整个数据集的熵Entropy：

• 因为整个数据集只有两个类别，他们的分布概率分别是\(\frac{9}{14}\)和\(\frac{5}{14}\)，所以根据Entropy是：\(Entropy(S)=-(\frac{9}{14}*log_2(\frac{9}{14})+\frac{5}{14}*log_2(\frac{5}{14}))=0.94\)

然后我们要考虑根据哪一个属性进行分裂，假设根据Outlook属性进行分裂，我们可以发现Outlook中有三个值，分别是：Sun,Rain,Overcast，分别计算他们的熵：
\(Entropy(S_{sun})=-(\frac{2}{5}*log_2(\frac{2}{5})+\frac{3}{5}*log_2(\frac{3}{5}))=0.971\)
\(Entropy(S_{overcast})=-(\frac{4}{4}*log_2(\frac{4}{4})+\frac{0}{4}*log_2(\frac{0}{4}))=0\)
\(Entropy(S_{rain})=-(\frac{3}{5}*log_2(\frac{3}{5})+\frac{2}{5}*log_2(\frac{2}{5}))=0.971\)
计算完三个Entropy后，来计算信息增益Information Gain：
\(IG(S,Outlook)=Entropy(S)-(\frac{5}{14}*Entropy(S_{sun})+\frac{5}{14}*Entropy(S_{overcast})+\frac{5}{14}*Entropy(S_{rain}))=0.246\)

用同样的道理，我们可以求出来剩下的几个特征的信息增益：
\(IG(S,Wind)=0.048\)
\(IG(S,Temperature)=0.0289\)
\(IG(S,Humidity)=0.1515\)
因为outlook这个作为划分的话，可以得到最大的信息增益，所以我们就用这个属性作为决策树的根节点，把数据集分成3个子集，然后再在每一个子集中重复上面的步骤，就会得到下面这样的决策树：

ID3的缺点

1. 如果样本中存在一个特征，这个特征中所有值都不相同（比方说是连续值的特征），这样可以想想的出假设用这个特征作为划分，那么信息增益一定是非常大的，因为所有的划分中都只会包含一个样本；对于具有很多值的属性它是非常敏感的，例如，如果我们数据集中的某个属性值对不同的样本基本上是不相同的，甚至更极端点，对于每个样本都是唯一的，如果我们用这个属性来划分数据集，它会得到很大的信息增益，但是，这样的结果并不是我们想要的。
2. ID3不能处理连续值属性；
3. ID3算法不能处理具有缺失值的样本；
4. 非常容易过拟合。

C4.5

对于有很多值得特征，ID3是非常敏感的，而C4.5用增益率Gain ratio解决了这个问题，先定义内在价值Intrinsic Value：

这个公式怎么理解呢？

• S就是数据集样本，\(|S|\)就是样本数量；
• a是某一个特征，比方说Outlook或者是Wind,然后\(v\in values(a)\)就是v就是a这个特征中的某一个值；
• \(|x\in S|value(x,a)=v|\)这个就是某一个特征a是v的样本数量；
  然后决策树之前使用信息增益Information Gain来作为分裂特征的选择，现在使用增益率IG rate：

可想而知，如果存在一个特征，比方说一个学生的学号（每一个学生的学号都不相同），如果用ID3选择学号进行分裂，那么一定可以达到非常大的信息增益，但是其实这是无意义过拟合的行为。使用C4.5的话，我们要计算IGR，这个学号的特征的内在价值IV是非常大的，所以IGR并不会很大，所以模型就不会选择学号进行分裂。

此外。C4.5可以处理连续值得划分，下面，我举例说明一下它的解决方式。假设训练集中每个样本的某个属性为：{65, 70, 70, 70, 75, 78, 80, 80, 80, 85, 90, 90, 95, 96}。现在我们要计算这个属性的信息增益。我们首先要移除重复的值并对剩下的值进行排序：{65, 70, 75, 78, 80, 85, 90, 95, 96}。接着，我们分别求用每个数字拆分的信息增益（比如用65做拆分：用≤65和>65≤65和>65做拆分，其它数字同理），然后找出使信息增益获得最大的拆分值。因此，C4.5算法很好地解决了不能处理具有连续值属性的问题。

C4.5如何处理缺失值

• 如果是训练数据中出现了缺失数据，那么就会考虑这个缺失数据所有可能的值。比方说一开始的数据库中，D1的Outlook变成了缺失值，那么D1的Outlook就会有\(\frac{4}{13}\)的概率是Sun，有\(\frac{4}{13}\)的概率是Overcast，有\(\frac{5}{13}\)的概率是Rain，然后其实也可以理解为这个样本就会变成3个样本，这三个样本有着不同的权重。
• 如果是在预测数据中出现了缺失数据，那么同样的，认为这个数据的这个缺失数据可能是任何可能的值，这个概率就是看决策树中Outlook划分的子集的样本数量。这个地方可能有点难懂，不理解的可以看这个博文：
  机器学习笔记（7）——C4.5决策树中的缺失值处理

C4.5对决策树的剪枝处理：
有两种剪枝处理方法，一个是预剪枝，一个是后剪枝，两者都是比较验证集精度，区别在于：

• 预剪枝：从上到下进行剪枝，如果精度没有提升，那么就剪掉，这个处理在训练模型的过程中进行；
• 后剪枝：从下到上进行剪枝，如果剪掉精度可以提升，就剪掉，这个处理过程是在模型训练结束之后再进行的。
  通常来说后者会比前者保留更多的分支，欠拟合的风险小，但是训练时间的开销会大一些。
  更具体地内容推荐这篇博文，讲的清晰易懂(没有必要看懂这个博文中的Python实现过程，毕竟现在sklearn库中都封装好了)：
  机器学习笔记（6）——C4.5决策树中的剪枝处理和Python实现

CART

分类回归树Classification and Regression Trees与C4.5的算法是非常相似的，并且CART支持预测回归任务。并且CART构建的是二叉树。

【面试考】【入门】决策树算法ID3，C4.5和CART

原文：https://www.cnblogs.com/PythonLearner/p/12945292.html