if (n <= 1) return n;
else return Fibonacci(n-1) + Fibonacci(n-2);
指数级的复杂度。给一个大n,就会overflow。
我想到的方法就是,从n=1开始循环求n=n+1时候的Fibonacci值,给一个for循环
public int Fib( int n){
int fibonacci = 1;
int a = 1; int b = 1;
if(n==0) return 0;
if (n==1|| n==2) return fibonacci;
for(int i=3; i<=n; i++){
fibnacci = a+b;
b = a;
a = fibnacci;
}
}
看GitHub上说这不是最简便的方法,此方法的复杂度是n,GitHub给出了复杂度为 lg n 的方法
这道题比较考验对Fibonacci数列的求解知识,涉及数学哦。
Fibonacci数列的求解用到了矩阵,f(n) =二维矩阵 {1110} 的n-1次方的左上角的值
关于Fibonacci数列求解的通项公式和矩阵求解方法,在另一篇
现在的问题转换为求矩阵{1, 1, 1, 0}的乘方。如果简单第从0开始循环,n次方将需要n次运算,并不比前面的方法要快。但我们可以考虑乘方的如下性质:
/ a^(n/2) * a^(n/2) n为偶数时
a^n=
\ a^((n-1)/2) * a^((n-1)/2) * a n为奇数时
要求得n次方,我们先求得n/2次方,再把n/2的结果平方一下。如果把求n次方的问题看成一个大问题,把求n/2看成一个较小的问题。这种把大问题分解成一个或多个小问题的思路我们称之为分治法。这样求n次方就只需要logn次运算了。
实现这种方式时,首先需要定义一个2×2的矩阵,并且定义好矩阵的乘法以及乘方运算。
原理: 观察: a(n) = a(n - 1) + a(n - 2) = 2 * a(n - 2) + a (n - 3) = 3 * a(n - 3) + 2 * a(n - 4) = 5 * a(n - 4) + 3 * a(n - 5) = ... ... = a(k) * a(n - k + 1) + a(k - 1) * a(n - k) 1、若令 n = 2k 得 a(2k) = a(k) * a(k + 1) + a(k-1) * a(k) = a(k) * [a(k) + a(k - 1)] + a(k-1) * a(k) = a(k) ^ 2 + 2 * a(k) * a(k - 1) 2、若令 n = 2k - 1 得 a(2k - 1) = a(k) * a(k) + a(k - 1) * a(k - 1) = a(k) ^ 2 + a(k - 1) ^ 2
##题目 一只青蛙一次可以跳上一级台阶,也可以一次跳上两级台阶,问n级台阶有几种跳法
##分析
每次只能跳一级或者跳两级,那么调N个台阶就可以分解为
先跳1级,然后剩余的是跳一个$N - 1$级的台阶,
先跳2级,然后剩余的是跳一个$N - 2$级的台阶,
那么它的递推公式为
##题目 一只青蛙一次可以跳一级台阶,可以跳两级台阶,可以跳三级台阶,....,可以跳n级台阶。问,n级台阶有几种跳法
##分析
n=1,有一种方法
n=2,一次一级或一次两级,即f(2-1)+f(2-2)
n=3,一次一级或一次两级或一次三级,即f(3-1)+f(3-2)+f(3-3)
n, f(n) = f(n-1) + f(n-2) + f(n-3) + ... + f(1) + f(0)
f(n-1) = f(n-2) + f(n-3) + ... + f(1)
f(n) = f(n-1) + f(n-2) + f(n-3) + ... + f(1)
= f(n-1) + f(n-1)
= 2*f(n-1)
已知f(1) = 1, f(0) = 0
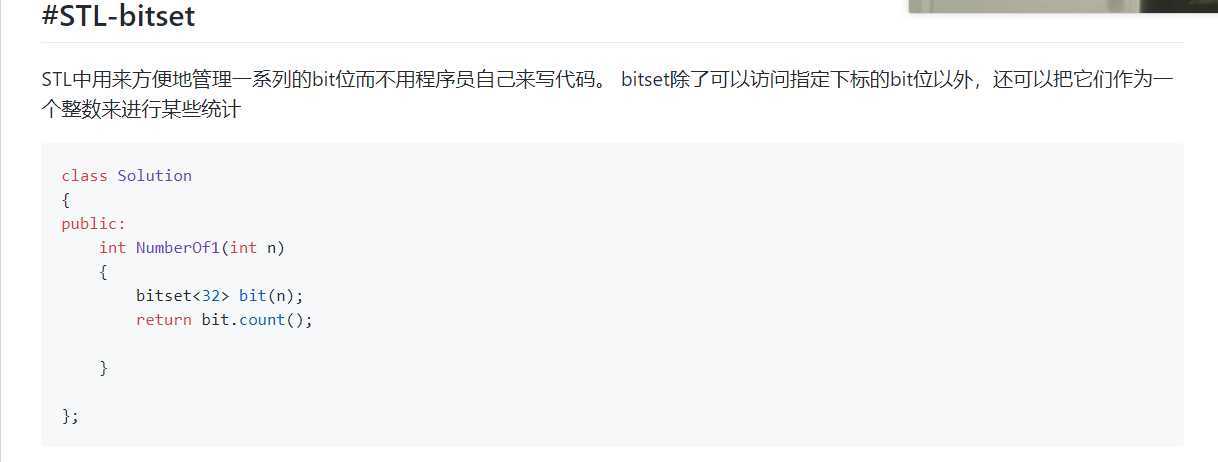
##题目 输入一个整数,输出对应二进制中1的个数,负数用补码表示
分析
可以进行移位,依次检测位上数字是否为1. 问题在于,逻辑/算数 左移/右移,符号位对四种情况的影响是不同,为了避免负数时的死循环,可以移动测试位而不移动数字,移动的终止条件是溢出,这时符号位无法被计算在内,所以需要单独测试符号位。
public int countOne(int n){
int count = 0;
long flag = 1;
while(flag < INT_MAX)
if(n && flag != 0)
count ++;
flag <<=;
if (n && flag != 0) //flag溢出后,单独测试符号位
count ++;
return count;
}
进阶算法:
思考,当一个二进制数字减1,会发生:这串二进制最右边的1会变成0,1后面的0都变为1.
举个例子:101100,从右往左数第三位就是最右边的1,当1100减1,会发生:最右边的1变0,后面的0变1,也就是101011.也就是橘色部分
用减1后的二进制串与原二进制串进行与运算,会发生:与结果从最右边的1开始全部为0,也就是101000
所以,若原二进制不为0,则至少有一个1;若与运算结果不为0,则说明源字符串还剩至少一个1
于是乎。通过计算该字符串能够进行几次与运算,来找到字符串中1的个数
while(n != 0){
count ++;
n &= (n-1);
}
return count;
原文:https://www.cnblogs.com/cherry-BAIL/p/12940600.html