传送门:https://www.luogu.com.cn/problem/P1600
NOIP2016D2T3
思路1:
统计每位玩家路上各个观察者观测到他的次数
树上路径?树链剖分?似乎有点无从下手
思路2:
统计每个观察者观察到的玩家数量
当然不能对每个观察者把所有路径枚举一遍来计算观测到的玩家数量
考虑到 树上路径比较烦人,不妨把它拆成两段,一段上升路径,一段下降路径
即(A->B)拆分成(A->LCA(A,B)->B) LCA(A,B)代表A 和 B的最近公共祖先 下同
实际上这也是许多算法处理树上路径(树剖,倍增LCA)的方法
这样一来,分别统计每个观测者观测到的上行时的玩家和下行时的玩家即可
令观察者所在节点为t,某玩家的起点和终点分别为u和v
那么显然,如果观察者能观察到玩家,那么u或v至少有一个在t的子树里
对于上行路径
我们注意到,观测者是否可以观测到某个上行者和观测者的观测时间和上行者与观测者的距离有关
而距离则等于观测者和上行者深度差
如果t在的观测者可以观测到玩家,那么u一定在t的子树里且w[t]=dep[u]-dep[t]
为了等式中的两个t在同一边,移项得
w[t]+dep[t]=dep[u]
对于下行路径
满足v一定在t的子树里且w[t]=dist(u,v)-(dep[v]-dep[t])时,观察者才能观测到下行者
移项得w[t]-dep[t]=dist(u,v)-dep[v]
无论上行路径还是下行路径,以上条件都只是可以观测到的必要 不充分条件
然而这样统计还有两个问题
想要变成充要条件还要加一条dep[LCA(u,v)]<=dep[t]
如下图,t根本不会被路径(u,v)经过,即使满足方程,t也无法收到u和v的贡献
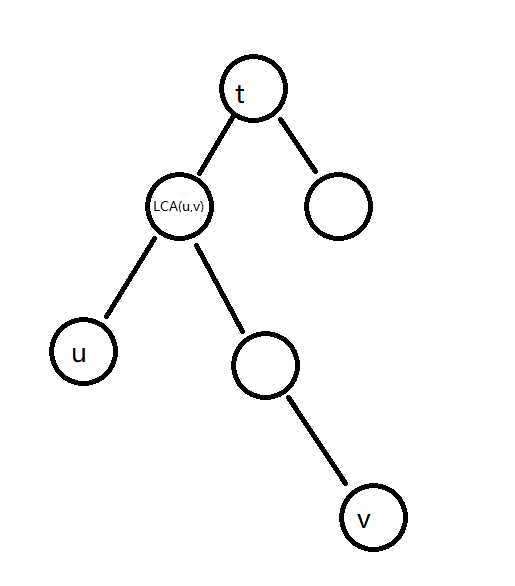
当然一位 以u为起点,以v为终点 的玩家如果恰好被在LCA(u,v)的观察者观察到,那么t的答案就会被u和v各统计一次
这两个问题稍后再讨论
现在的主要问题时如何对每个观测者统计符合等式的节点数
观察一下这两个等式
上行:w[t]+dep[t]=dep[u]
下行:w[t]-dep[t]=dist(u,v)-dep[v]
含有t的已经被移到了左边,含有u v的全部在右边
这样一来,统计每个节点的答案就很简单了
相当于送快递的把快递按照楼层分进了若干个桶里,取件的时候只需要在所在的楼层对应的桶里找就行了
对于上行路径,w[t]+dep[t]就是t的楼层,只有dep[u]=楼层的时候t才能收到来自u的贡献
开俩数组bu,bd
bu[i]用来累计dep[u]=i的节点u的数量
bd[i]用来累计dist(u,v)-dep[v]==i的v 的数量
遍历t前后 t对应的桶(即bu[w[t]+dep[t]]和bd[w[t]-dep[t]])的变化量即为t的答案
现在我们希望跑一遍dfs即可出来所有答案,那么具体怎么dfs?
每遍历到一个节点就bu[dep[u]]+=(以u为起点的玩家数量)
然后遍历以u为终点的所有玩家,对于每个玩家 执行 bd[玩家路径长度-dep[u]]++
为了能够找到所有以u为终点的玩家,我们当然不能开n个数组
可以考虑用链表存储(类似于邻接链表)。如果你懒得写链表,也可以用vector,不过会很慢
接下来是刚才留下的两个问题
先考虑dep[LCA(u,v)]>dep[t]的情况
不妨采取这种思路:统计完一个节点的答案后,在桶中删除所有以他为LCA的玩家的贡献
为了能够找到这些路径,我们还得开链表或者vector来存这些东西
接下来考虑t=LCA(u,v)的情况
可以考虑提前结算掉这一部分“错账”
对于所有的玩家,设起点为u,终点为v,t=LCA(u,v),只要w[t]+dep[t]=dep[u],且w[t]-dep[t]=dist(u,v)-dep[v] (还是刚才的两个等式,其实满足一个等式另外一个就满足了)
则ans[LCA(u,v)]--;
这个万恶的毒瘤题目就讨论完了,接下来就是代码
#include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #define clr(x,y) memset(x,y,sizeof(x)) const int N=3e5+5; struct Edge { int to,next; Edge() {next=0; } Edge(int tu,int nxt) {to=tu; next=nxt; } }; struct LList { Edge edge[N*2]; int cnt,head[N]; LList() { clr(edge,0); cnt=0; } void add(int x,int y) { edge[++cnt]=Edge(y,head[x]); head[x]=cnt; } }; #define forl(i,v,l,x) for (int i=l.head[x],v=l.edge[i].to;i;i=l.edge[i].next,v=l.edge[i].to) int n,m; struct Graph { LList edge,pt,pm; int w[N],bu[N<<1],t_bd[N<<1],ans[N],top[N],size[N],hson[N],fa[N],dep[N],spcnt[N],dist[N],ss[N],ts[N]; int *bd; Graph() { clr(bu,0); clr(t_bd,0); clr(ans,0); clr(spcnt,0); bd=t_bd+N; } void dfs1(int x) { size[x]=1; hson[x]=0; int mxsize=0; forl (i,y,edge,x) if (y!=fa[x]) { fa[y]=x; dep[y]=dep[x]+1; dfs1(y); size[x]+=size[y]; if (size[y]>mxsize) mxsize=size[hson[x]=y]; } } void dfs2(int x,int tp) { top[x]=tp; if (!hson[x]) return; dfs2(hson[x],tp); forl (i,y,edge,x) if (y!=fa[x] && y!=hson[x]) dfs2(y,y); } void slpf(int root) { fa[root]=dep[root]=0; dfs1(root); dfs2(root,root); } int lca(int x,int y) { while (top[x]!=top[y]) { if (dep[top[x]]<dep[top[y]]) std::swap(x,y); x=fa[top[x]]; } if (dep[x]<dep[y]) std::swap(x,y); return y; } void solveDfs(int x) { if (x==6) printf(""); ans[x]-=bu[w[x]+dep[x]]+bd[w[x]-dep[x]]; forl (i,y,edge,x) if (y!=fa[x]) solveDfs(y); bu[dep[x]]+=spcnt[x]; forl (i,p,pt,x) bd[dist[p]-dep[x]]++; ans[x]+=bu[w[x]+dep[x]]+bd[w[x]-dep[x]]; forl (i,p,pm,x) bu[dep[ss[p]]]--,bd[dist[p]-dep[ts[p]]]--; } void solve(int root=1) { slpf(root); for (int i=1;i<=m;i++) { int lsa=lca(ss[i],ts[i]); pt.add(ts[i],i); pm.add(lsa,i); dist[i]=dep[ss[i]]+dep[ts[i]]-2*dep[lsa]; spcnt[ss[i]]++; if (w[lsa]+dep[lsa]==dep[ss[i]]) ans[lsa]--; } solveDfs(root); } } graph; int main() { scanf("%d%d",&n,&m); for (int i=1;i<n;i++) { int a,b; scanf("%d%d",&a,&b); graph.edge.add(a,b); graph.edge.add(b,a); } for (int i=1;i<=n;i++) scanf("%d",&graph.w[i]); for (int i=1;i<=m;i++) scanf("%d%d",&graph.ss[i],&graph.ts[i]); graph.solve(); for (int i=1;i<=n;i++) printf("%d ",graph.ans[i]); return 0; }
AC!

原文:https://www.cnblogs.com/LMXZ/p/12900694.html