联考20200520 T1 石子游戏

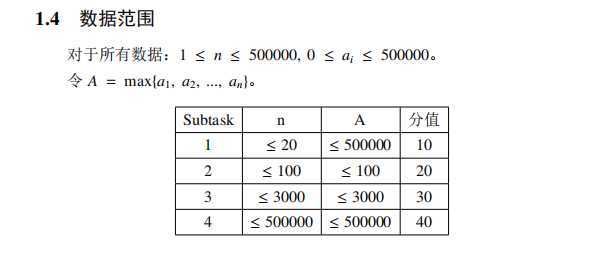
分析：
考虑一个奇妙的性质：当最大的石子为\(A\)时，需要删去最少的而保证后手必胜的石子堆的数量是\(logA\)级别的（线性基是\(log\)级别的）
于是就变得可做起来了
本来的过程是异或背包，可以使用\(FWT\)优化整个过程
最坏情况也只会做\(logA\)次FWT
复杂度\(O(Alog^{2}A)\)

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<iostream>
#include<map>
#include<string>

#define maxn 1000005
#define INF 0x3f3f3f3f
#define MOD 1000000007
#define inv2 500000004

using namespace std;

inline long long getint()
{
	long long num=0,flag=1;char c;
	while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1;
	while(c>=‘0‘&&c<=‘9‘)num=num*10+c-48,c=getchar();
	return num*flag;
}

int n;
int a[maxn];
int A[maxn],B[maxn];
int len,mx,sum;

inline int add(int x,int y){return x+y<MOD?x+y:x+y-MOD;}
inline void FWT_xor(int *a,int opt)
{
	for(int i=1;i<len;i<<=1)for(int j=0;j<len;j+=i<<1)for(int k=0;k<i;k++)
	{
		int X=a[j+k],Y=a[i+j+k];
		a[j+k]=add(X,Y);a[i+j+k]=add(X,MOD-Y);
	}
}

int main()
{
	n=getint();
	for(int i=1;i<=n;i++)mx=max(a[i]=getint(),mx),sum^=a[i];
	if(!sum){printf("%d\n",n);return 0;}
	while(mx)mx>>=1,len++;
	len=1<<len;
	A[0]=1;
	for(int tim=1;;tim++)
	{
		for(int i=1;i<=n;i++)B[a[i]]++;
		FWT_xor(A,1),FWT_xor(B,1);
		for(int i=0;i<len;i++)A[i]=1ll*A[i]*B[i]%MOD;
		FWT_xor(A,-1);
		if(A[sum]){printf("%d\n",n-tim);return 0;}
		for(int i=0;i<len;i++)B[i]=0;
	}
}

联考20200520 T1 石子游戏

原文：https://www.cnblogs.com/Darknesses/p/12925840.html