\(KMP\) 算法

\(1.\) 算法概述

给定长度为 \(n\) 的文本串 \(text\)，以及长度为 \(m\) 的模式串 \(pattern\)

\(KMP\) 算法可以在 \(O(m)\) 时间内预处理出 \(pattern\) 的所有真前缀和真后缀中最大的公共长度

进而在 \(O(n + m)\) 时间内判断 \(text\) 中是否出现 \(pattern\)，并求出 \(pattern\) 在 \(text\) 中出现的所有位置

\(2.\) 算法详解

\(2.1\) 真后缀与真前缀

不包含串本身的后缀叫做真后缀

不包含串本身的前缀叫做真前缀

\(2.2\) 蛮力算法的局限性

蛮力算法的局限性在于，每次失配，都要重头再来匹配，如下图所示

\(2.3\) \(KMP\)

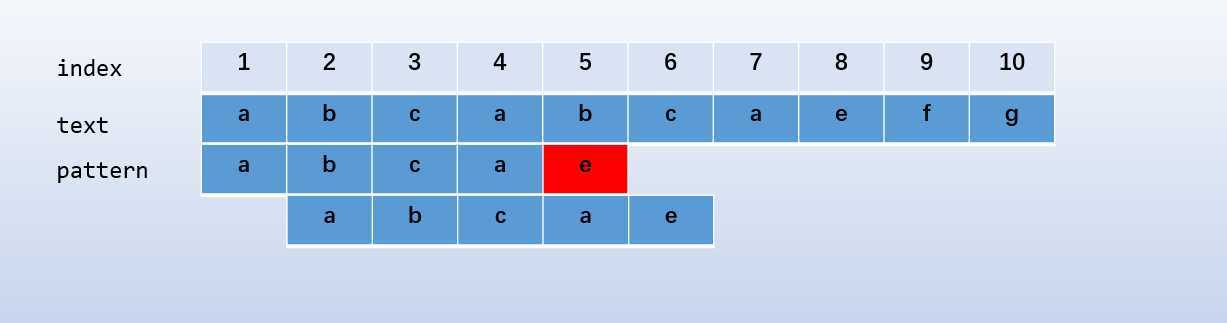
一个显然的优化如下

经过观察发现，这样的优化是基于如下事实

对于字符串 \(abca\)，其所有真前缀和真后缀中最大的公共长度为 \(1\)，相应的真前缀与真后缀均为 \(a\)

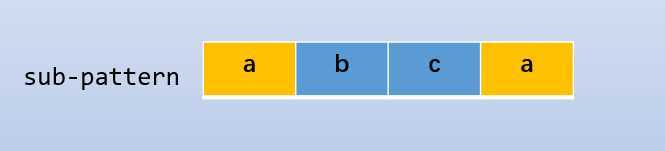
所以我们不必从头匹配，只需要将 \(pattern[1] = a\) 的后一项，即 \(pattern[2] = b\) 和模式串中的 \(b\) 继续匹配即可

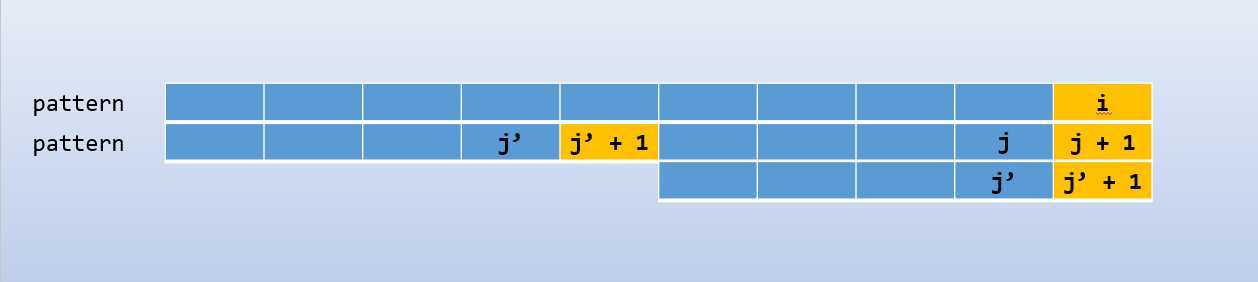
更加普遍的，示例如下

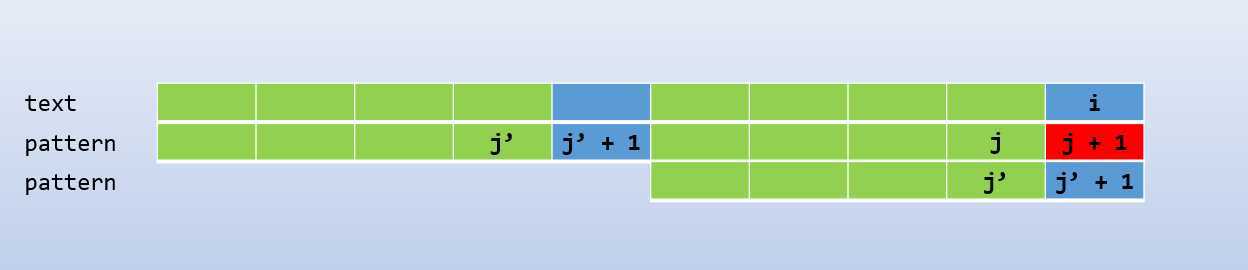
如图所示，\(text[i]\) 和 \(pattern[j + 1]\) 失配，而绿色部分为相同的字符串，所以只需要将 \(j\) 指向 \(j‘\) 即可继续匹配

利用好真后缀与真前缀的信息，便是 \(KMP\) 的关键所在

代码如下

int L1 = strlen(text + 1);
for(int i = 1, j = 0; i <= L1; ++i) {
    while(j && text[i] != pattern[j + 1]) j = Next[j];
    if(text[i] == pattern[j + 1]) ++j;
    if(j == L2) printf("%d\n", i - L2 + 1);
}

\(2.4\) \(Next\) 数组

\(Next\) 数组用于求解 \(pattern\) 的所有真前缀和真后缀中最大的公共长度

设 \(pattern = abcabce\)，对应的 \(Next\) 数组示例如下

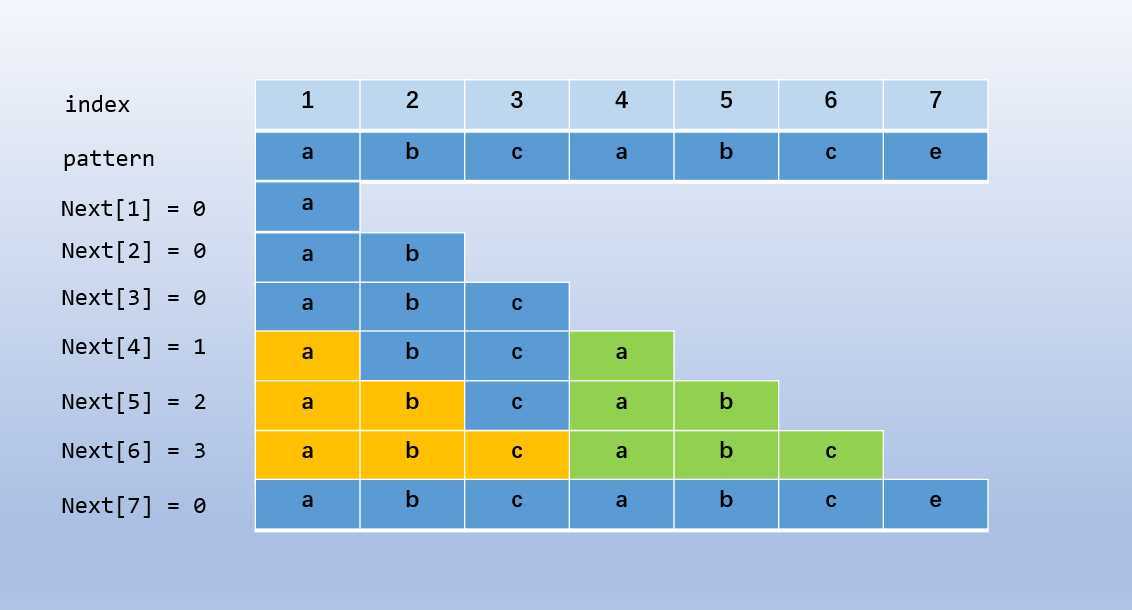
考虑求解 \(Next\) 数组

首先初始化 \(Next[1]\)，令 \(Next[1] = 0\)

基于动态规划的思想，若 \(pattern[i] = pattern[j+1]\)，那么 \(Next[i] = Next[j] + 1\)

若 \(pattern[i] \neq pattern[j]\)，只需要令 \(j = next[j]\) 即可

代码如下

int L2 = strlen(pattern + 1);
Next[1] = 0;
for(int i = 2, j = 0; i <= L2; ++i) {
    while(j && pattern[i] != pattern[j + 1]) j = Next[j];
    if(pattern[i] == pattern[j + 1]) Next[i] = ++j;
}

\(3.\) 代码

#include <bits/stdc++.h>
#define fi first
#define se second
#define pii pair<int, int>
#define pb push_back
#define dbg(a, l, r) for(int i = l; i <= r; ++i) printf("%d%c", a[i], " \n"[i == r])
typedef long long LL;
typedef unsigned long long ULL;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const LL MOD = 11092019;
const int inf = 0x3f3f3f3f;
const int DX[] = {0, -1, 0, 1, 0, -1, -1, 1, 1};
const int DY[] = {0, 0, 1, 0, -1, -1, 1, 1, -1};
const int N = 1e6 + 7;
const double PI = acos(-1);
const double EPS = 1e-6;
using namespace std;
using namespace std;

inline LL read() //读入函数
{
    char c = getchar();
    LL ans = 0, f = 1;
    while(!isdigit(c)) {if(c == ‘-‘) f = -1; c = getchar();}
    while(isdigit(c)) {ans = ans * 10 + c - ‘0‘; c = getchar();}
    return ans * f;
}

char text[N], pattern[N];
int Next[N];
void KMP(char *text, char *pattern, int *Next)
{
    int L1 = strlen(text + 1), L2 = strlen(pattern + 1);
    Next[1] = 0;
    for(int i = 2, j = 0; i <= L2; ++i) {
        while(j && pattern[i] != pattern[j + 1]) j = Next[j];
        if(pattern[i] == pattern[j + 1]) Next[i] = ++j;
    }
    for(int i = 1, j = 0; i <= L1; ++i) {
        while(j && text[i] != pattern[j + 1]) j = Next[j];
        if(text[i] == pattern[j + 1]) ++j;
        if(j == L2) printf("%d\n", i - L2 + 1);
    }
    dbg(Next, 1, L2);
}
int main()
{
    scanf("%s %s", text + 1, pattern + 1);
    KMP(text, pattern, Next);
    return 0;
}

$KMP$ 算法

原文：https://www.cnblogs.com/ChenyangXu/p/12920218.html