The statement of this problem is the same as the statement of problem C1. The only difference is that, in problem C1, nn is always even, and in C2, nn is always odd.
You are given a regular polygon with 2⋅n2⋅n vertices (it‘s convex and has equal sides and equal angles) and all its sides have length 11 . Let‘s name it as 2n2n -gon.
Your task is to find the square of the minimum size such that you can embed 2n2n -gon in the square. Embedding 2n2n -gon in the square means that you need to place 2n2n -gon in the square in such way that each point which lies inside or on a border of 2n2n -gon should also lie inside or on a border of the square.
You can rotate 2n2n -gon and/or the square.
The first line contains a single integer TT (1≤T≤2001≤T≤200 ) — the number of test cases.
Next TT lines contain descriptions of test cases — one per line. Each line contains single odd integer nn (3≤n≤1993≤n≤199 ). Don‘t forget you need to embed 2n2n -gon, not an nn -gon.
Print TT real numbers — one per test case. For each test case, print the minimum length of a side of the square 2n2n -gon can be embedded in. Your answer will be considered correct if its absolute or relative error doesn‘t exceed 10−610−6 .
3 3 5 199
1.931851653 3.196226611 126.687663595
n是奇数的情况其实本质上就是把n是偶数的情况造出的边与多边形的边平行的正方形转个角度。
类似下图:
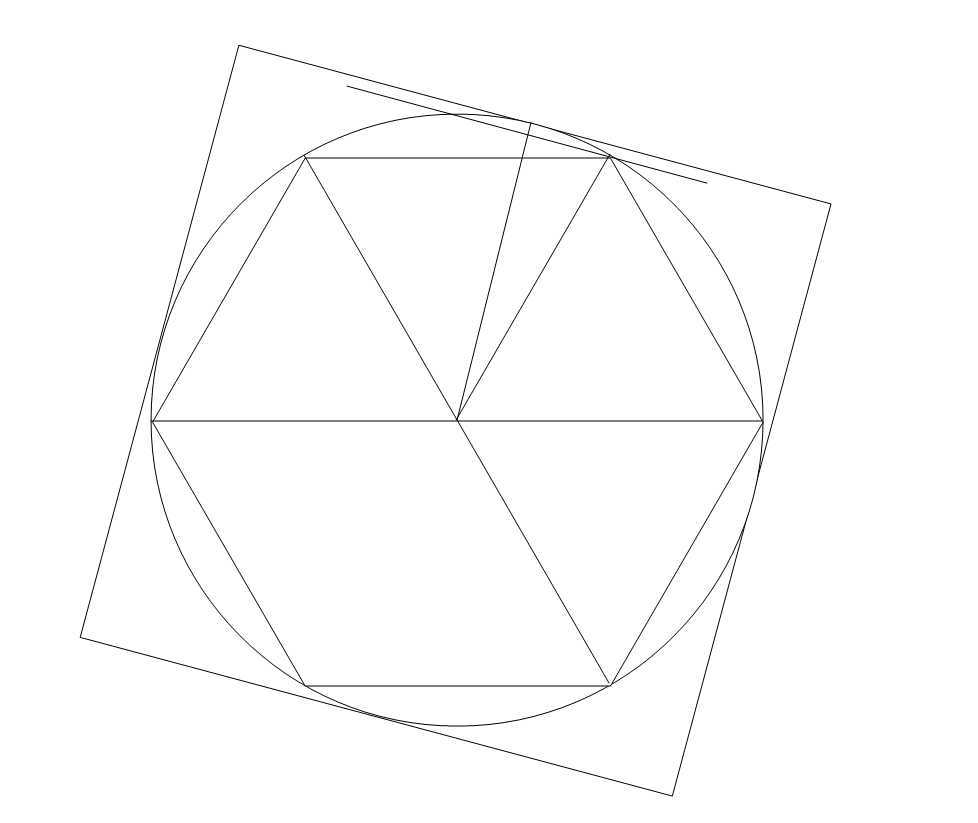
由对称性可得,当转过的角度等于1/4内部小三角形的顶角时边长最小
(也可以列函数式,转过的角度范围为0~1/4小三角形顶角,边长的表达式关于x单调递减..)
#include <bits/stdc++.h> #define PI 3.1415926535898 using namespace std; int main() { int t; cin>>t; while(t--) { int n; cin>>n; double ang=360.0/(2*n); ang/=2.0; double ans=0.0; ans=0.5/sin(ang/180.0*PI)*cos(0.5*ang/180.0*PI)*2; printf("%.9lf\n",ans); } }
Educational Codeforces Round 87 (Rated for Div. 2) C2. Not So Simple Polygon Embedding(几何)
原文:https://www.cnblogs.com/lipoicyclic/p/12906649.html