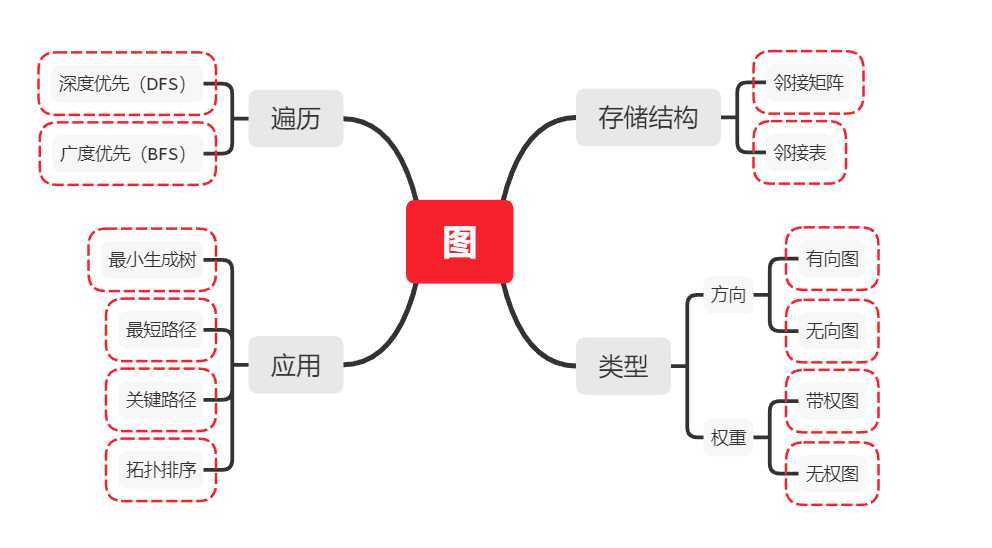
图是由表示顶点的集合v和表示顶点之间关系的集合E组成的,通常表示为:G=(v,E),
其中,G表示一个图,v是图G中顶点的有穷非空集合,E是图G中边的有限集合。
E(G)也可以为空集。若E(G)为空,则图G只有顶点而没有边。
路径长度:顶点序列上经过的边的个数。
入度:以顶点V为弧头的弧的数目称为该顶点的入度,
出度:以顶点V为弧尾的弧的数目称为该顶点的出度,记作OD(V)。
顶点V的度为:TD(V)=ID(V)+OD(V)
有向完全图:有n(n-1)条边(图中每个顶点和其余n-1个顶点都有弧相连)。
无向完全图:有n(n-1)/2条边(图中每个顶点和其余n-1个顶点都有边相连)。
定义:
逻辑结构分为两部分:V和E集合,其中,V是顶点,E是边。
因此,用一个一维数组存放图中所有顶点数据;用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。
邻接矩阵数据类型定义:

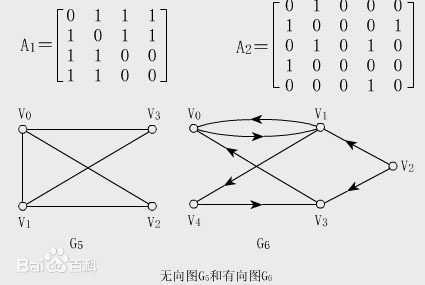
邻接表数据类型定义:

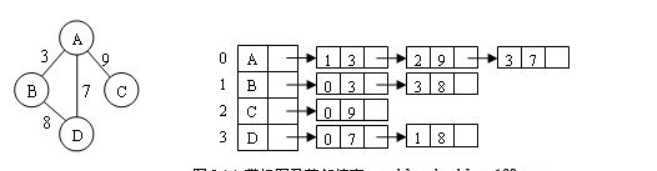
(1)从某个顶点V出发,访问顶点并标记为已访问
(2)访问V的邻接点,如果没有访问过,访问该顶点并标记为已访问,然后再访问该顶点的邻接点,递归执行
如果该顶点已访问过,退回上一个顶点,再检查该顶点的邻接点是否都被访问过,如果有没有访问过的继续向下访问,如果全部都访问过继续退回到上一个顶点,继续同样的步骤。
深度优先遍历类似于树的先序遍历,深度优先遍历算法结果不唯一。
(1)从某个顶点V出发,访问该顶点的所有邻接点V1,V2..VN
(2)从邻接点V1,V2...VN出发,再访问他们各自的所有邻接点
(3)重复上述步骤,直到所有的顶点都被访问过
Kruskal算法
Kruskal算法是基于贪心的思想得到的。
首先我们把所有的边按照权值先从小到大排列,接着按照顺序选取每条边,如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止。
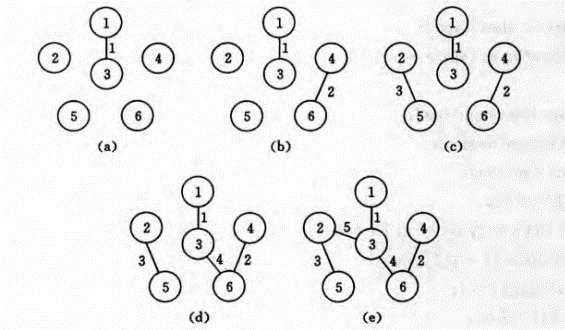
Prim算法
从某一顶点出发,依次访问该点的邻接点,找到权值最小边,直到全部访问完。
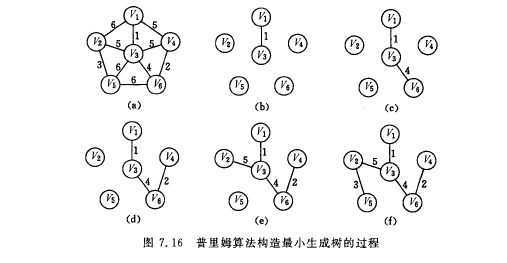
从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径——最短路径。
1.Floyd算法

2.Dijkstra算法

对拓扑排序的不唯一性刚开始存在一定的问题,比如下面这个例子
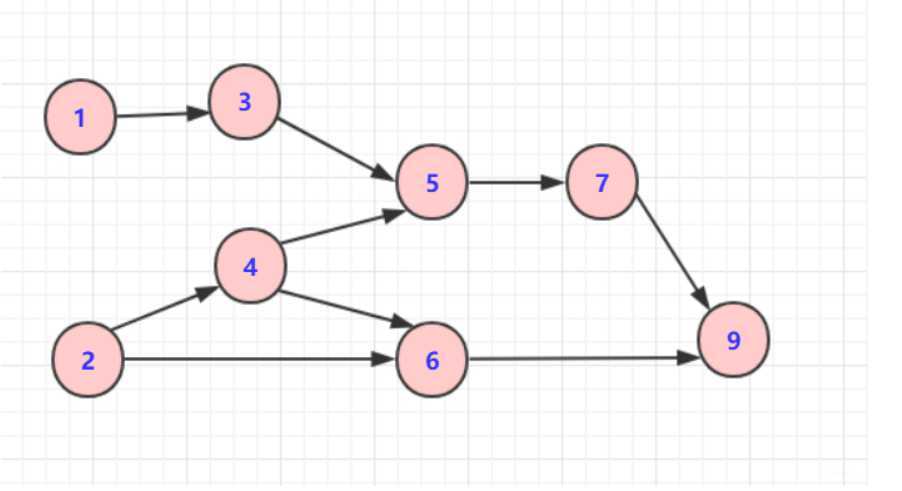
排序结果(不唯一):
2 4 1 3 5 7 6 9
1 2 4 3 6 5 7 9
通过几个例子,明白了主要思路就是找到一个没有前驱的结点并且删除它,一直到没有结点为止。
原文:https://www.cnblogs.com/254916-cn/p/12906566.html