Codeforces Round #643 (Div. 2) 题解 （佛系更新中）

https://codeforces.com/contest/1355

A. Sequence with Digits

这题我会证！首先对于百位来说，不可能从x跳到x+2，只能从x变成x+1或者不变（因为最大变化量为 \(9\times9=81\)）

这样的话大约1000次内，百位不可避免地从9变成0，这样min的值是0，变化量min*max就是一直是0了

#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll;
#define int ll
int a,k;
string s;
signed main(){
	int T; cin>>T;
	while(T--){
		cin>>a>>k;
		while(--k){
			s=to_string(a);
			int x=*min_element(s.begin(),s.end())-48;
			int y=*max_element(s.begin(),s.end())-48;
			if(x==0)break;
			a+=x*y;
		}
		cout<<a<<endl;
	}
	return 0;
}

B. Young Explorers

比赛中我自始至终都以为所有探险者都要组队，然后emmm...

贪心，尽量组规模小的队，所以排个序就好了

感谢zkx巨佬提供的代码（没错，我懒了补题）

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+7;

int n;
int a[N];

inline void solve() {
  cin >> n;
  for (int i = 1; i <= n; ++i) {
    cin >> a[i];
  }
  sort(a+1, a+n+1);
  int res = 0;
  for (int i = 1, cnt = 0; i <= n; ++i) {
    ++cnt;
    if (cnt >= a[i]) {
      ++res;
      cnt = 0;
    }
  }
  cout << res << endl;
}

signed main() {
  ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
  int T = 1;
  cin >> T;
  for (int t = 1; t <= T; ++t) {
    solve();
  }
  return 0;
}

C. Count Triangles

先讲一下我的思路

\(A≤x≤B≤y≤C≤z≤D\)

因为 \(x\) 范围不大，考虑枚举 \(x\) 的值。这样对于任意满足要求的 \(y\)，都有 \(C\le z\le \min(D,x+y-1)\)，或者说，\(z\) 的方案数为 \(\max(0,\min(D,x+y-1)-C+1)\)。令这个东西为 \(f(y)=\max(0,\min(D,x+y-1)-C+1)\)，函数图像大概长这样

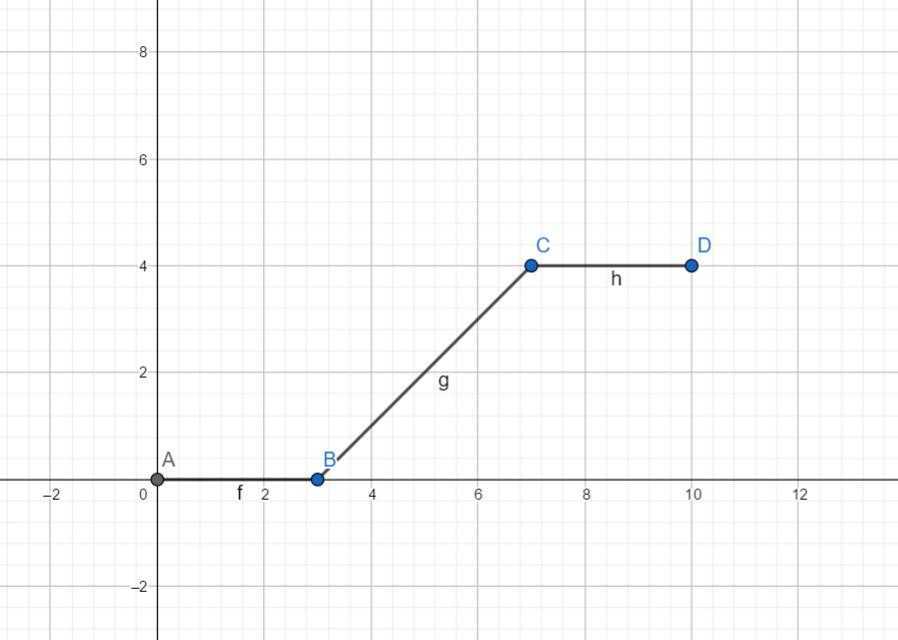
先一次函数上升，然后变成常函数。此时就能成两段讨论（一次函数和常函数），求出两个交点什么的，太过于数学，逃了

#include <bits/stdc++.h>
using namespace std;
#define repeat(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define repeat_back(i,a,b) for(int i=(b)-1,_=(a);i>=_;i--)
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
const int N=200010; typedef long long ll;
#define int ll
int a,b,c,d;
signed main(){
	cin>>a>>b>>c>>d;
	int ans=0;
	repeat(i,a,b+1){
		int x=max(c,i+b-1);
		int y=min(i+c-1,d);
		int l=x-c+1,r=y-c+1;
		if(x<=y)ans+=(l+r)*(r-l+1)/2; //一次函数（等差数列求和）
		if(i+c-1>d)ans+=(i+c-1-d-1)*(d-c+1); //常函数
	}
	cout<<ans<<endl;
	return 0;
}

Codeforces Round #643 (Div. 2) 题解 （佛系更新中）

原文：https://www.cnblogs.com/axiomofchoice/p/12902895.html