*digital exam (DE)*, *multiple choice*
Lecture content:
Informally: Given an initial state, a goal state (or set of goal states) and a set of available actions. Find a sequence of actions that take you from the initial state to the goal state.

Tree search VS graph search:
Tree search can visit a state multiple times. And as such it will explore the "sub tree" found after this state several times, which can be expensive. Graph search fixes this by keeping track of all visited states in a closed list. If a newly found successor to next is already known, it won‘t be inserted into the open list

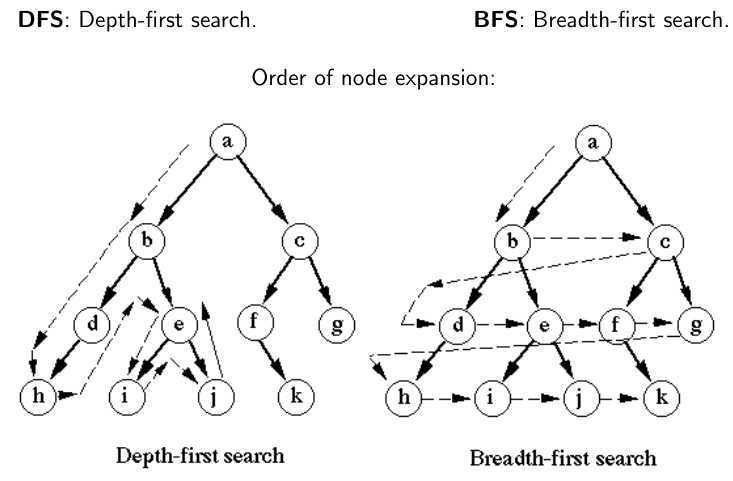
The search has two types of nodes:
• Expanded nodes: Nodes for which all children have been generated.
• Frontier: Nodes that have been generated, but for which we haven’t yet computed the children.


Best-first search strategies with Graph-Search
Best-first search:
• Frontier is a priority queue where the key of a node n is denoted f (n).
• choose a node n from frontier : extract minimal node from priority queue, that is, a node n with minimal f (n).
• add child m to frontier: insert node into priority queue.

The most widely known form of best-first search is called A∗ search (pronounced “A-star search”). It evaluates nodes by combining g(n), the cost to reach the node, and h(n), the cost to get from the node to the goal:
f(n)=g(n)+h(n).
A∗search is both complete and optimal.
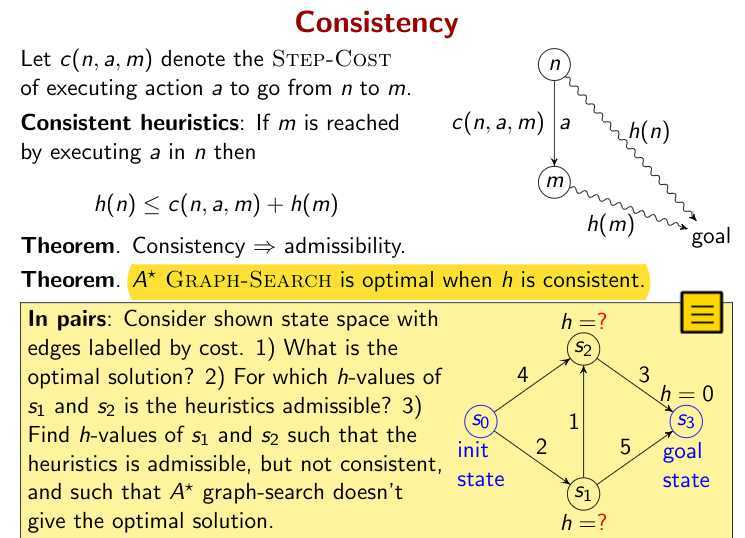
Conditions for optimality: Admissibility and consistency

原文:https://www.cnblogs.com/dulun/p/12897691.html