2.1 线性组合
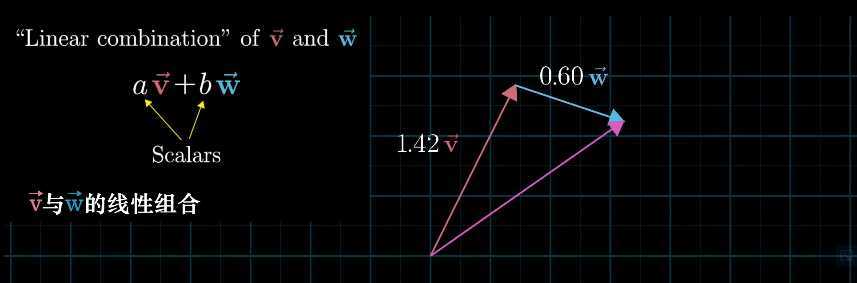
定义：向量 
及 
的线性组合（Linear Combination）为 
。
线性组合的各种情况：
- （线性的含义）固定一个向量，让另外一个向量自由伸缩，那么所产生向量的终点最终落在一条直线上 ;
- 让两个向量自由移动，这样加和后我们就能得到所有可能的向量
- 如果两个向量共线时，这样所产生的的向量就会固定在一条过原点的直线上
- 如果两个向量都是零向量，这样始终保持在原点
2.2张成的空间
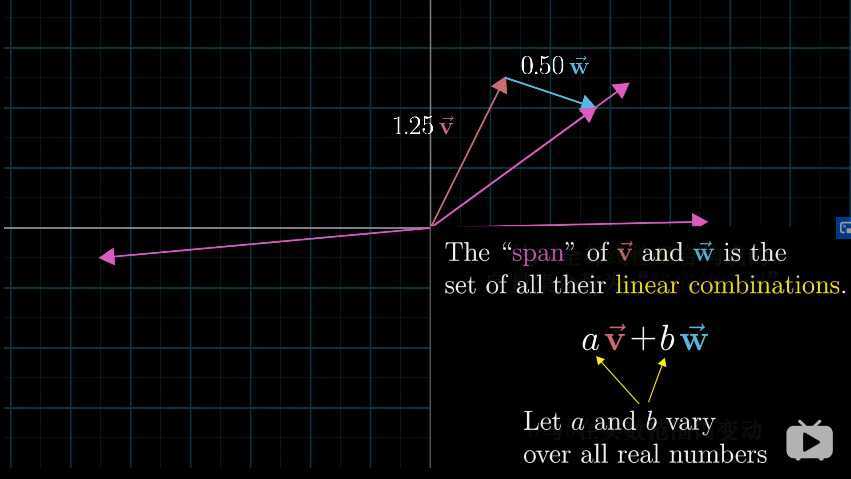
定义：向量 及 的的全部线性组合（Linear Combination, ）构成的向量空间称为“张成(Span)的空间”，实际上，对于张成空间而言，就是让 
在实数空间中自由变化，删掉张成空间中的一个向量不会影响结果。
线性组合对应的张成空间：
固定一个向量，让另外一个向量自由伸缩，那么所产生向量的终点最终落在一条直线上，张成的空间为直线；
让两个向量自由移动，这样我们就能得到所有可能的向量，张成的空间为整个空间
如果两个向量都是零向量，这样始终保持在原点，张成的空间为原点。
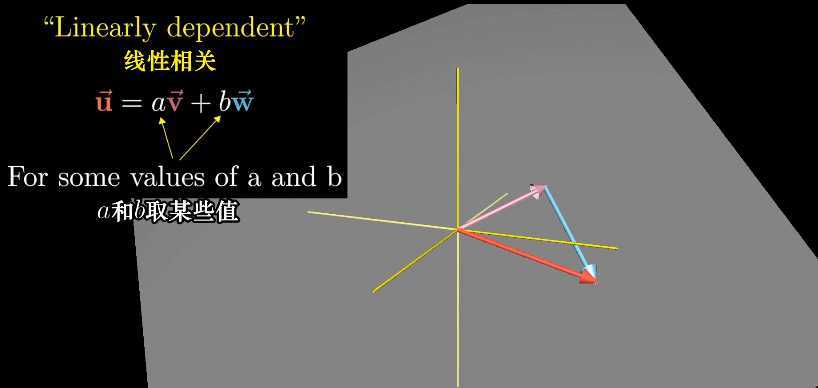
（一）线性相关：
- 如果两个向量共线时，这样所产生的的向量就会固定在一条过原点的直线上，这样就意味着存在一个多余的向量，删掉其中一个向量不会影响张成的空间。当这种情况发生时，我们就成为“线性相关（Linear dependent，
），意味着向量可以用其他向量的线性组合来表示，因为该向量已经落在了线性组合张成的空间中”
（二）线性无关：
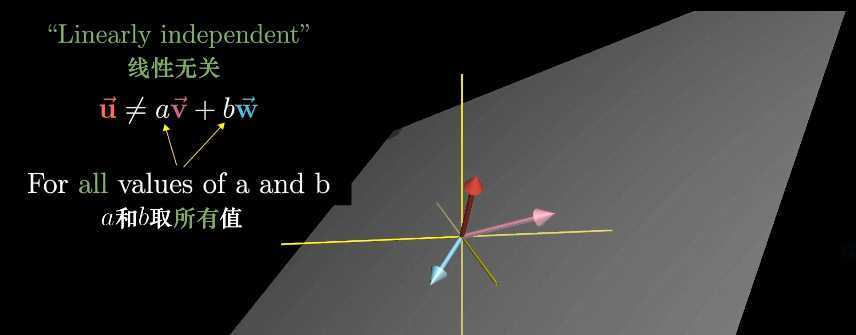
如果所有向量给张成的空间添加了新的维度，我们就称为“线性无关（Linear independent， 
）”，
2.3 基 basis
向量空间中的基是张成该空间中的一个线性无关的向量集合。
2.4 向量的另一种表示形式
利用基向量的线性组合表示向量
如：在二维空间中，设基向量 
这个过程过程相当于对基向量进行了缩放，然后进行加和的结果。
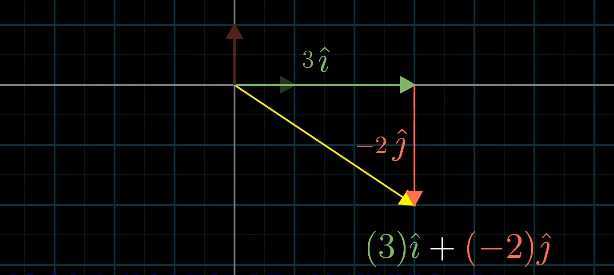
那么，我们可以选择不同的向量基，进而构建一个合理的坐标系。
2.5 总结
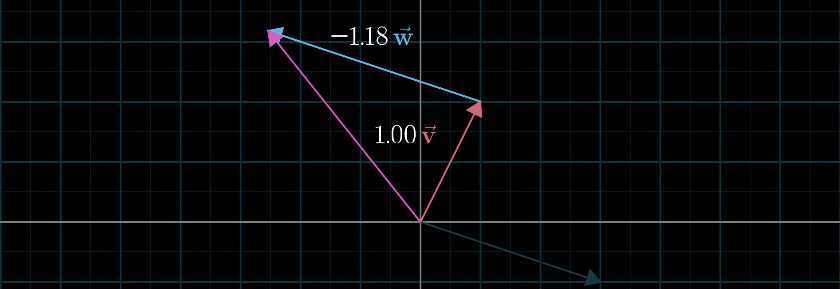
因此，这样就建立起了线性组合、张成空间&基之间的关系：
- 线性组合全部的向量集合能够构成张成空间；
- 线性无关的向量集合构成了空间的基。
线性代数的本质(2)——线性空间、张成的空间&基
原文：https://www.cnblogs.com/wkfvawl/p/12879973.html
