ML-Review-L1、L2范数正则化

• L1 & L2范数

 正则化通过让原目标函数加上了所有特征系数绝对值的和来实现正则化，而 正则化通过让原目标函数加上了所有特征系数的平方和来实现正则化。

在更新w时，L1表现为，每次加上一个常数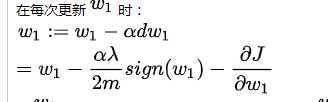

可能使得w变为0，代表该特征对预测没影响，也就使得特征变稀疏，起到特征选择的作用

L2表现为每次对特征系数w进行比例缩放，

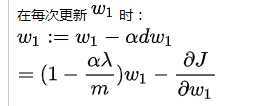
 模型也变简单，起到防止过拟合的作用

首先介绍一下范数的定义，假设 是一个向量，它的 范数定义:

在目标函数后面添加一个系数的“惩罚项”是正则化的常用方式，为了防止系数过大从而让模型变得复杂。在加了正则化项之后的目标函数为:

式中， 是一个常数， 为样本个数， 是一个超参数，用于控制正则化程度。

正则化时，对应惩罚项为 L1 范数 :

正则化时，对应惩罚项为 L2 范数:

从上式可以看出， 正则化通过让原目标函数加上了所有特征系数绝对值的和来实现正则化，而 正则化通过让原目标函数加上了所有特征系数的平方和来实现正则化。

两者都是通过加上一个和项来限制参数大小，却有不同的效果： 正则化更适用于特征选择，而 正则化更适用于防止模型过拟合。

让我们从梯度下降的角度入手，探究两者的区别。
为了方便叙述，假设数据只有两个特征即 ，考虑 正则化的目标函数：

在每次更新 时：


若 为正数，则每次更新会减去一个常数；若 为负数，则每次更新会加上一个常数，所以很容易产生特征的系数为 0 的情况，特征系数为 0 表示该特征不会对结果有任何影响，因此 正则化会让特征变得稀疏，起到特征选择的作用。

现考虑 正则化的目标函数：

在每次更新 时：


从上式可以看出每次更新时，会对特征系数进行一个比例的缩放而不是像 正则化减去一个固定值，这会让系数趋向变小而不会变为 0，因此正则化会让模型变得更简单，防止过拟合，而不会起到特征选择的作用。
以上就是 正则化的作用以及区别。

下面来看一个课程中的例子，当不使用正则化，发生过拟合时:

 

overfitting

 

在这里插入图片描述