题目:
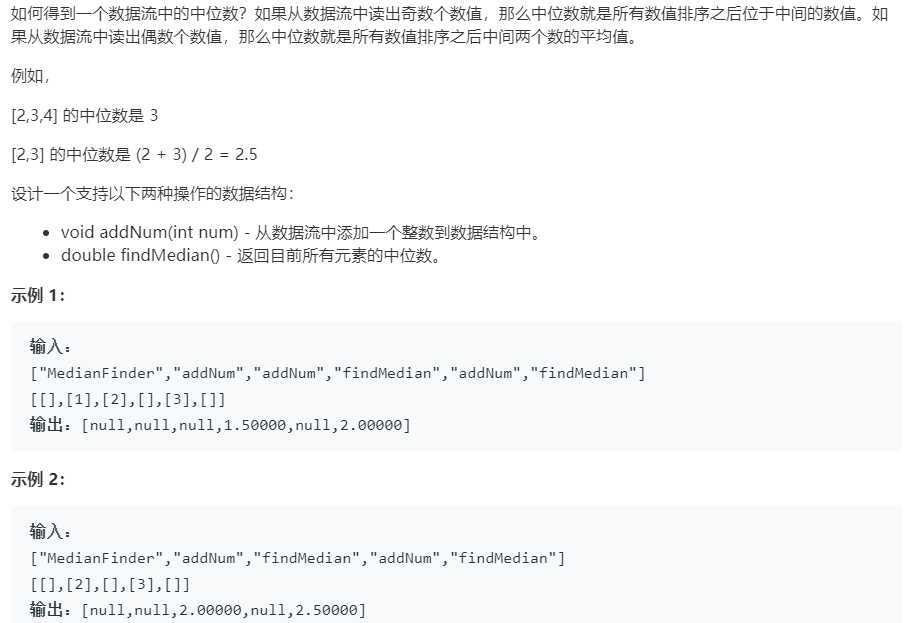
解答:
方法一:C++超时
1 class MedianFinder { 2 vector<double> store; 3 4 public: 5 // Adds a number into the data structure. 6 void addNum(int num) 7 { 8 store.push_back(num); 9 } 10 11 // Returns the median of current data stream 12 double findMedian() 13 { 14 sort(store.begin(), store.end()); 15 16 int n = store.size(); 17 return (n & 1 ? store[n / 2] : (store[n / 2 - 1] + store[n / 2]) * 0.5); 18 } 19 };
方法二:二分查找插入
方法一的缺点在于对数组进行了排序操作,导致时间复杂度较高,假如每次插入一个值前数组已经排好序了呢?这样我们只需考虑每次将值插在合适的位置即可,所以使用二分查找来找到这个合适的位置,会将时间复杂度降低到O(n)(查找: O(logn),插入: O(n))
1 class MedianFinder { 2 vector<int> store; // resize-able container 3 4 public: 5 // Adds a number into the data structure. 6 void addNum(int num) 7 { 8 if (store.empty()) 9 store.push_back(num); 10 else 11 store.insert(lower_bound(store.begin(), store.end(), num), num); // binary search and insertion combined 12 } 13 14 // Returns the median of current data stream 15 double findMedian() 16 { 17 int n = store.size(); 18 return n & 1 ? store[n / 2] : (store[n / 2 - 1] + store[n / 2]) * 0.5; 19 } 20 };
方法三:优先队列(堆)
我们将中位数左边的数保存在大顶堆中,右边的数保存在小顶堆中。这样我们可以在 {\mathcal{O}}(1)O(1) 时间内得到中位数。
1 class MedianFinder { 2 priority_queue<int> lo; // 大顶堆 3 priority_queue<int, vector<int>, greater<int>> hi; // 小顶堆 4 5 public: 6 // Adds a number into the data structure. 7 void addNum(int num) 8 { 9 lo.push(num); // 加到大顶堆 10 11 hi.push(lo.top()); // 平衡 12 lo.pop(); 13 14 if (lo.size() < hi.size()) { // 维护两个堆元素个数 15 lo.push(hi.top()); 16 hi.pop(); 17 } 18 } 19 20 // Returns the median of current data stream 21 double findMedian() 22 { 23 return lo.size() > hi.size() ? (double) lo.top() : (lo.top() + hi.top()) * 0.5; 24 } 25 };
原文:https://www.cnblogs.com/ocpc/p/12858559.html