题目:
解答:
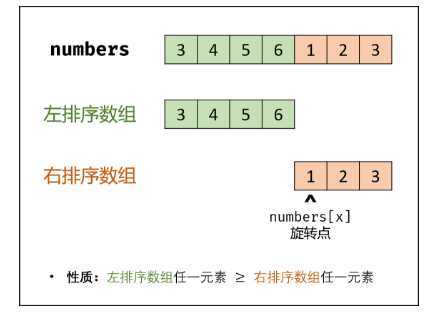
(1)如下图所示,寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 numbers[x] ,称 x 为 旋转点 。
(2)排序数组的查找问题首先考虑使用 二分法 解决,其可将遍历法的 线性级别 时间复杂度降低至 对数级别 。
算法流程:
(1)循环二分:设置 i, j 指针分别指向 numbers 数组左右两端,m = (i + j) // 2为每次二分的中点( "//" 代表向下取整除法,因此恒有i≤m<j ),可分为以下三种情况:
A. 当 numbers[m] > numbers[j]时: m 一定在 左排序数组 中,即旋转点 x 一定在 [m + 1, j]闭区间内,因此执行 i = m + 1;
B. 当 numbers[m] < numbers[j] 时: m 一定在 右排序数组 中,即旋转点 xx 一定在[i, m]闭区间内,因此执行 j = m;
C. 当 numbers[m] == numbers[j] 时: 无法判断 m 在哪个排序数组中,即无法判断旋转点 x 在 [i, m]还是 [m + 1, j]区间中。解决方案: 执行 j = j - 1缩小判断范围 (分析见以下内容) 。
(2)返回值:当i == j时跳出二分循环,并返回numbers[i]即可。
1 class Solution { 2 public: 3 int minArray(vector<int>& numbers) 4 { 5 int left = 0; 6 int right = numbers.size() - 1; 7 while (left < right) 8 { 9 int mid = left + (right - left) / 2; 10 if (numbers[mid] > numbers[right]) 11 { 12 left = mid + 1; 13 } 14 else if (numbers[mid] < numbers[right]) 15 { 16 right = mid; 17 } 18 else 19 { 20 right--; 21 } 22 } 23 24 return numbers[left]; 25 } 26 };
原文:https://www.cnblogs.com/ocpc/p/12856941.html