传送门:http://codeforces.com/contest/606/problem/E
解题思路:
可以证明最终选取的项目不会超过2个。可以在坐标轴上画图证明。将所有的$(a_{i},b_a{i})$视为二维坐标轴上的点$(x,y)$,对于任意两点$(x_{1},y_{1}),(x_{2},y_{2})$,将这两点连起来,所形成的的线段上任意一点为一天的可以获得的量。而最优解,必然是取其与点$(p,q)$的交点(若线段有交点),因为其他的点花费更大。可以先做个预处理,保证每个点只有左上和右下有点,其余的点删除(即不存在$x_{i}<y{i},x{j}<y_{j}$的情况,因为j肯定比x更优,i点不会用到)。
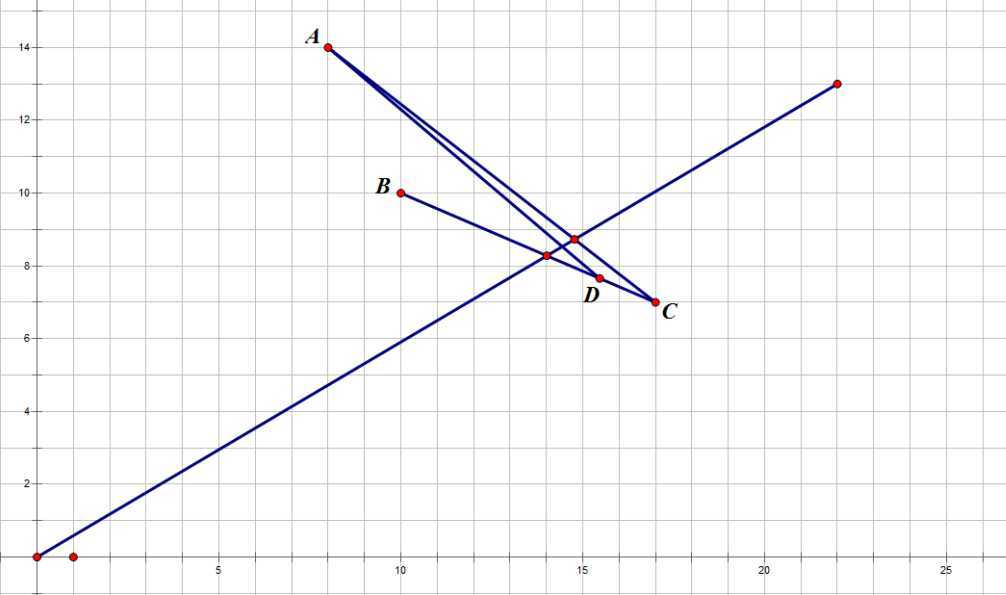
下面证明不存在三个项目:假设选取了三个项目A,B,C,如图所示,必然是连接了线段BC,然后在线段BC上取一点D,连接AD,最后取得是线段AD与点$(0,0)$和点$(p,q)$所形成的的直线的交点。可以看成,如果AC一定比AD跟优,因为B点一定在他下方,因此不存在三点以上情况,只有两点构成。在仔细想一下,一定是凸包上相邻两个点与该点的交点。所以,我们可以求一个凸包,然后计算凸包相邻两点所形成的线段(注意,是线段,不是直线,这里wa了一发)的交点,形成的交点就是单天的获取方案。直接p除以其横坐标即可。当然这是取两个项目的情况,取一个项目的暴力判断一下即可,取min即可。
比赛的时候发现自己凸包的板子写的天花乱坠,既没有类封装,也没有函数封装,打了半天没打出来。
最后贴上AC代码。
#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; typedef pair <double,double> pii; #define rep(i,x,y) for(int i=x;i<y;i++) #define rept(i,x,y) for(int i=x;i<=y;i++) #define per(i,x,y) for(int i=x;i>=y;i--) #define all(x) x.begin(),x.end() #define pb push_back #define fi first #define se second #define mes(a,b) memset(a,b,sizeof a) #define mp make_pair #define dd(x) cout<<#x<<"="<<x<<" " #define de(x) cout<<#x<<"="<<x<<"\n" #define debug() cout<<"I love Miyamizu Mitsuha forever.\n" const int inf=0x3f3f3f3f; const int maxn=1e5+5; pii p[maxn]; bool comp1(const pii &s1,const pii &s2) { return s1.se>s2.se||(s1.se==s2.se&&s1.fi>s2.fi); } pii point[maxn]; double dis(const pii &s1,const pii &s2) { return sqrt((s1.fi-s2.fi)*(s1.fi-s2.fi)+(s1.se-s2.se)*(s1.se-s2.se)); } pii operator -(const pii &s1,const pii &s2) { return mp(s1.fi-s2.fi,s1.se-s2.se); } double chaji(const pii &s1,const pii &s2) { return s1.fi*s2.se-s1.se*s2.fi; } bool comp(const pii &s1,const pii &s2) { double x=chaji(s1-point[0],s2-point[0]); if( x>0|| (x==0&&fabs(s1.fi-point[0].fi)<fabs(s2.fi-point[0].fi)) ) return 1; else return 0; } int graham(pii point[],int n)//计算凸包 { int p=0,cnt=0; rep(i,1,n) if( point[i].se<point[p].se||(point[i].se==point[p].se&&point[i].fi<point[p].fi) ) p=i; swap(point[0],point[p]); sort(point+1,point+n,comp); cnt=2; rep(i,2,n) { while(cnt>=2&&chaji( point[cnt-1]-point[i],point[cnt-2]-point[i] )>=0 ) cnt--; point[cnt++]=point[i]; } return cnt; } double a,b; pii node(pii s1,pii s2) { double x=( (s1.se*s2.fi-s1.fi*s2.se)/(s2.fi-s1.fi) )/(b/a-(s2.se-s1.se)/(s2.fi-s1.fi)); double y=b/a*x; return mp(x,y); } int main() { ios::sync_with_stdio(false); cin.tie(0); int n; cin>>n>>a>>b; rep(i,0,n) cin>>p[i].fi>>p[i].se; sort(p,p+n,comp1); int cnt=0; p[cnt++]=p[0]; double mal=p[0].fi; rep(i,1,n) { if(p[i].fi<=mal) continue; mal=p[i].fi; p[cnt++]=p[i]; } n=cnt; if(n==1) { cout<<fixed<<setprecision(10)<<max(a/p[0].fi,b/p[0].se);//仅有一点时,无法计算凸包,特判 return 0; } cnt=graham(p,n); double ans=1e18; rep(i,0,cnt-1) { pii point=node(p[i],p[i+1]);//计算交点 if(point.fi<=p[i].fi&&point.fi>=p[i+1].fi) ans=min(ans,a/point.fi);//交点在线段上才可以选取 } rep(i,0,cnt) ans=min(ans,max(a/p[i].fi,b/p[i].se));//取单点的情况 cout<<fixed<<setprecision(10)<<ans<<"\n"; return 0; }
codeforces 606 E. Freelancer's Dreams(凸包)
原文:https://www.cnblogs.com/FZUzyz/p/12847029.html