它其实就是一个 BST(Binary Search Tree 二叉搜索树)。
当然,不同的平衡树会有自己的特性
只有一个:任意一个节点的左子树的所有节点都比它的优先级高,右子树的所有节点都比他的优先级低。
注意:一个节点也可以当成一颗子树
如下:
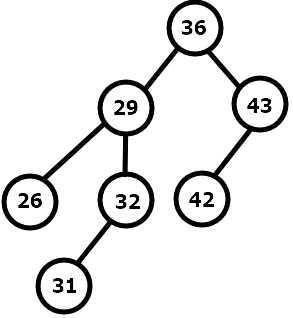
看到这里你也许会想:既然平衡树就是一颗 BST ,那还要它干嘛?
看这里:
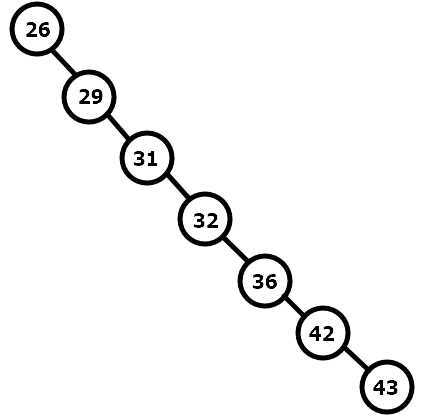
由于 BST 可能会退化成一条链,使得原本 \(O(log n)\) 的速度退化成 \(O(n)\)
于是,大佬们发明了各种各样的平衡树,避免 BST 退化成一条链
当然这里只是最常用的
还有更多的平衡树等待着你去学习、发明
| 操作 | 时间复杂度 |
|---|---|
| 插入元素 | \(O(log n)\) |
| 弹出元素 | \(O(log n)\) |
| 查询排名 | \(O(log n)\) |
| 查询第 K 大 | \(O(log n)\) |
| 查询前驱 | \(O(log n)\) |
| 查询后继 | \(O(log n)\) |
当然这些是基础功能,还有更多的以后会讲到
这是一个最适合新手学习的
包含区间反转、可持久化
FHQ Treap
这个也是必须要掌握的
包含区间反转、 LCT
更新中...
The End
原文:https://www.cnblogs.com/KonjakLAF/p/12754844.html