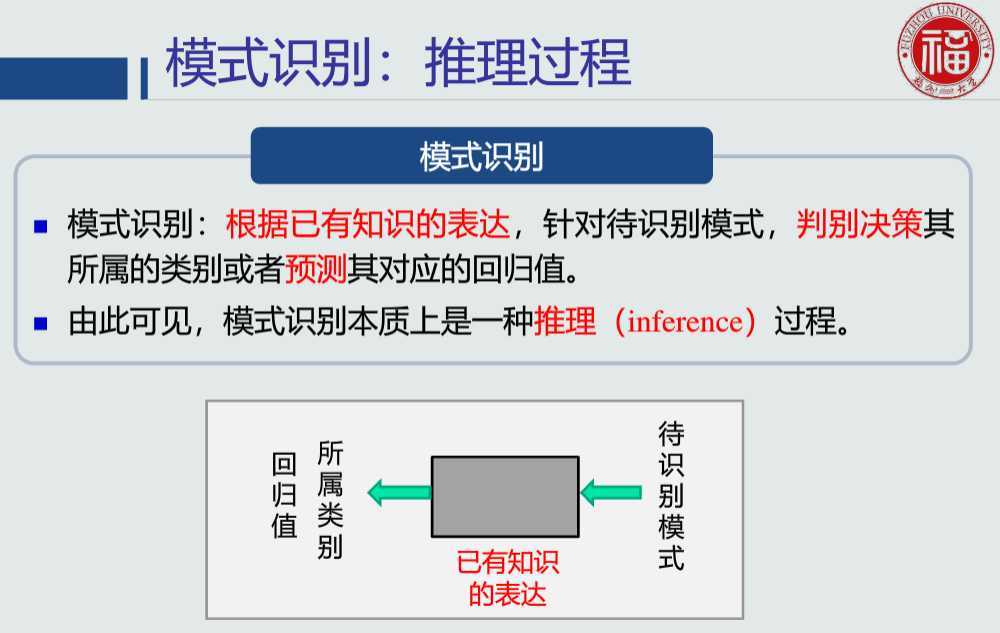
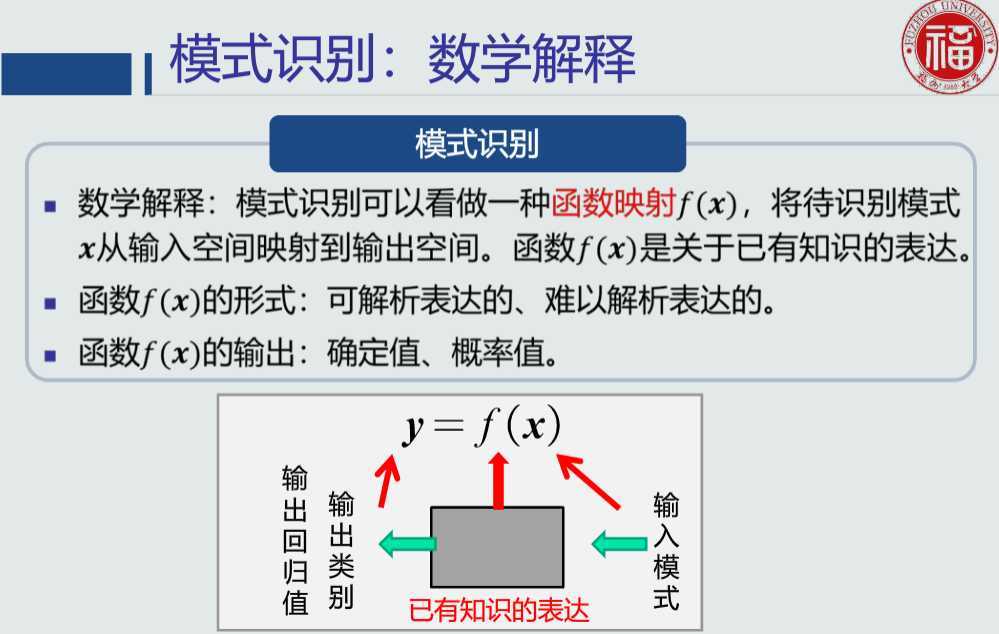
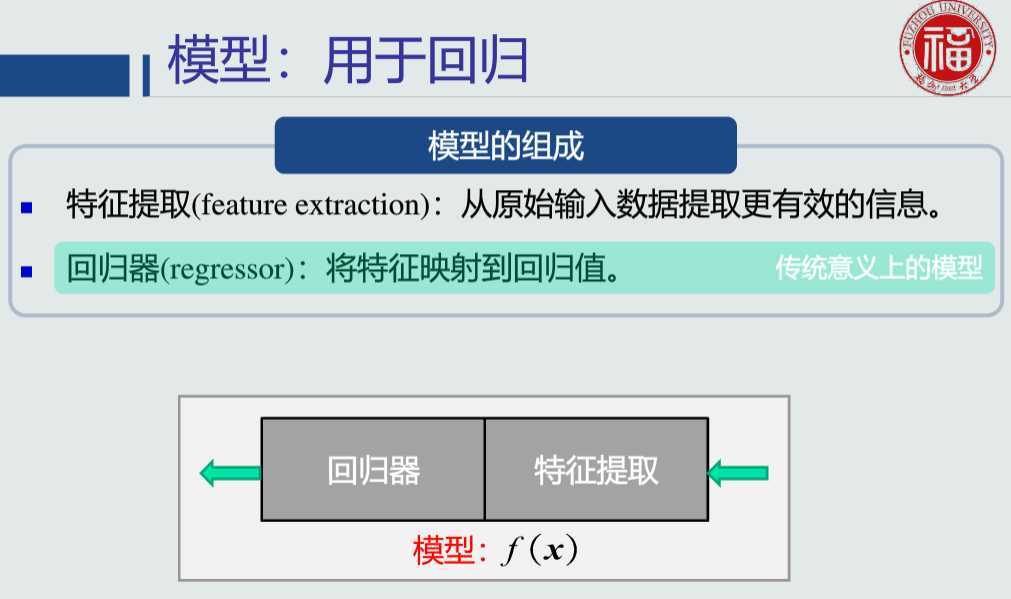
所谓模式识别的问题就是用计算的方法根据样本的特征将样本划分到一定的类别中去。模式识别就是通过计算机用数学技术方法来研究模式的自动处理和判读,把环境与客体统称为“模式”。随着计算机技术的发展,人类有可能研究复杂的信息处理过程,其过程的一个重要形式是生命体对环境及客体的识别。模式识别以图像处理与计算机视觉、语音语言信息处理、脑网络组、类脑智能等为主要研究方向,研究人类模式识别的机理以及有效的计算方法。

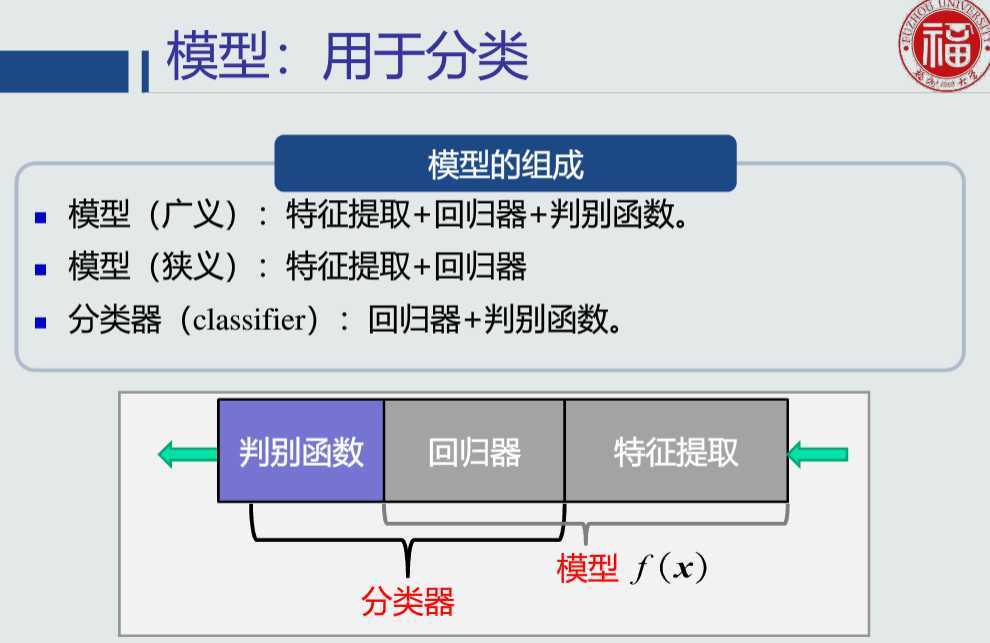
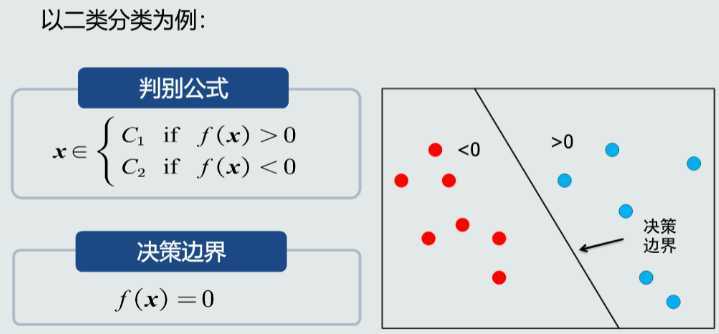
判别函数是指各个类别的判别区域确定后,可以用一些函数来表示和鉴别某个特征矢量属于哪个类别,这些函数就称为判别函数。这些函数不是集群在特征空间形状的数学描述,而是描述某一位置矢量属于某个类别的情况,如属于某个类别的条件概率,一般不同的类别都有各自不同的判别函数。




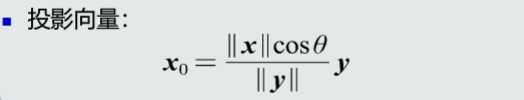

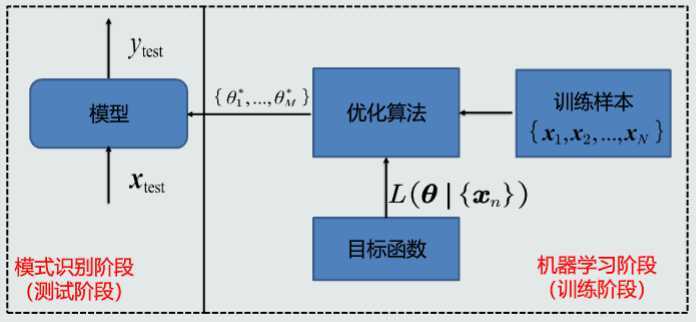
训练样本的目的是 数学模型的参数,经过训练之后,可以认为你的模型系统确立了下来。
建立的模型有多好,和真实事件的差距大不大,既可以认为是测试样本的目的。
一般训练样本和测试样本相互独立,使用不同的数据。



留出法

K折交叉验证
将数据集随机分为k份,每次不重复地取一份作为测试集,其余作为训练集,重复k次,最后取这k次地统计指标作为评估结果。
留一验证

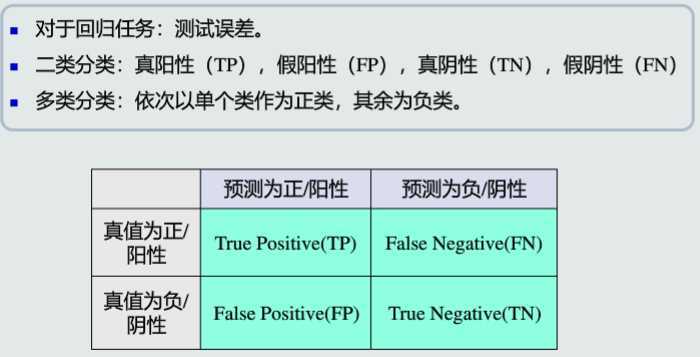
基本概念
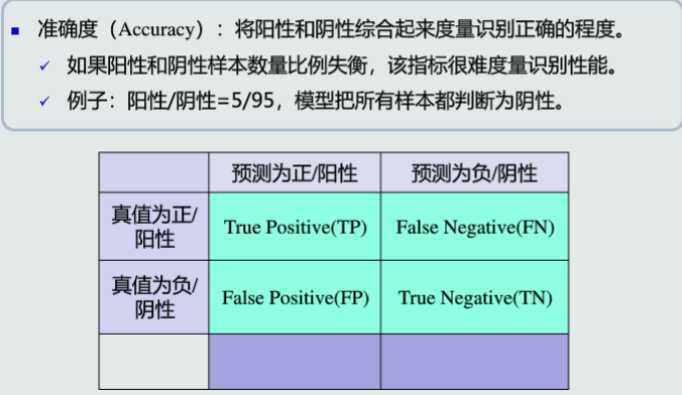
准确度
精度&召回率
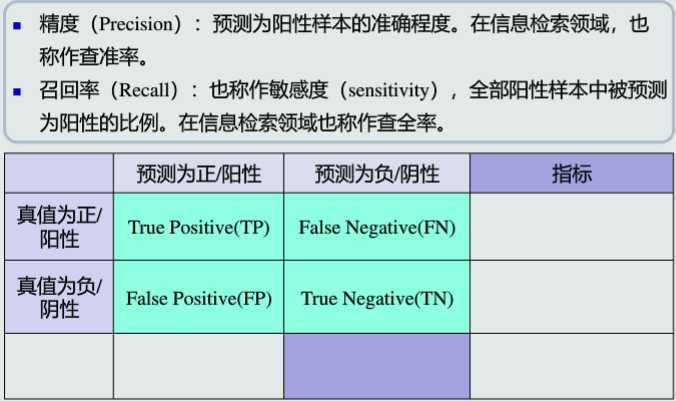
F-Score

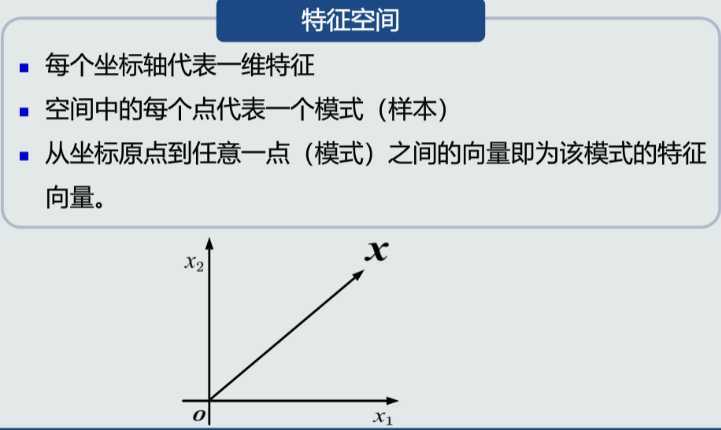
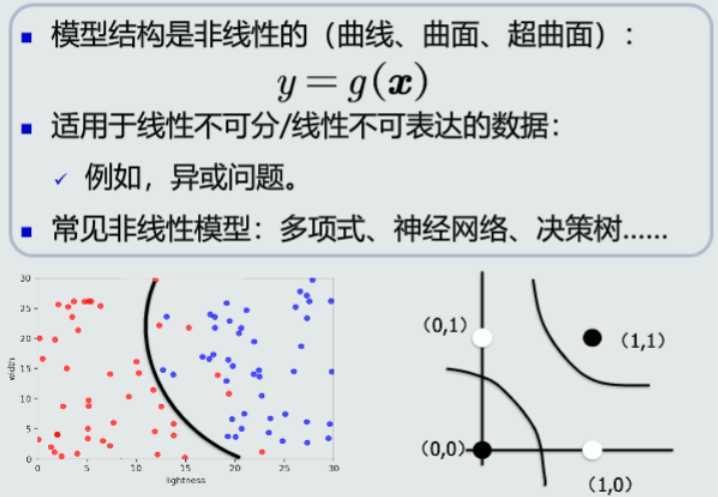
物体识别实际上是通过模式识别来实现的,现实生活中的很多时候,区分两个物体的不同,并不是靠最本质的区别来判定的,因为会很复杂或者麻烦。所以要借助一些其他的特征来判定。因此实际上,模式识别并不是根据物体本身来判断的,而是根据被感知到的某些性质,容易感知到的某些物体特征来进行判别。也就引出了模式的定义——如物体的颜色、厚度、大小、重量等的易被感知到的物体特性,叫做模式。 为了识别物体,也就是进行分类,一般会用分类器这个工具。故而分类器实际上识别的不是物体,而是物体的模式。
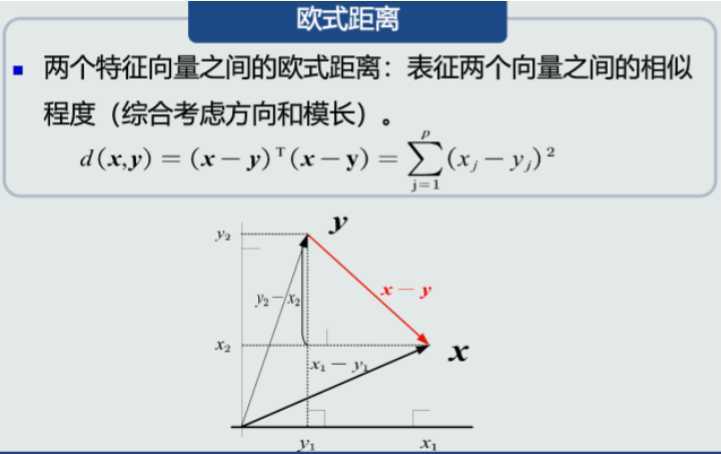
MED分类器,即最小欧拉距离(Mininal Euclidean Distance)分类器,它选取类中样本均值作为类的原型,将待预测样本判断为与其欧拉距离最小的类
二分类决策边界:

在高维空间中,该决策边界是一个超平面,且该平面垂直且二分连接两个类原型的线。
由于只考虑到类原型的距离,不考虑类样本的分布,可能出现反直觉或错误的结果,如:
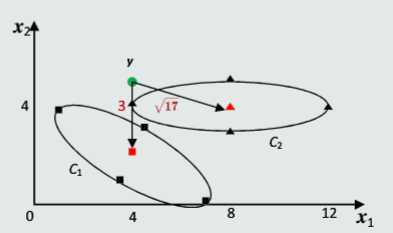
白化的目的是去除输入数据的冗余信息。


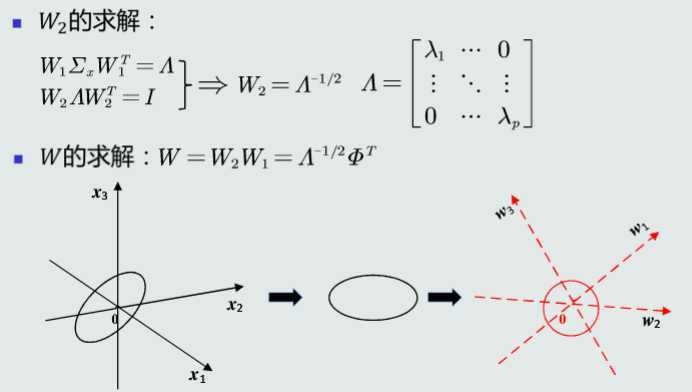

MICD分类器,即最小类内距离(Minimal Intra-Class Distance)分类器由MED分类器演化而来,同样采用均值作为类的原型,但采用马氏距离作为距离度量。将待预测样本判断为与其马氏距离最小的类。
二分类决策边界:

决策边界为超平面、超球面、超椭球面、超抛面或者超双曲面。
此分类器采用马氏距离,综合考虑了类的不同特征之间的相关性和尺度差异
但在均值相同时,趋向于选择方差较大的类,因为方差较大会使\(∑^{?1}\)较小
学习了基于距离的分类器及特征白化的原理和思想,把测试样本到每个类之间的距离作为决策模型,将测试样本判定为其距离最近的类。距离衡量为欧式距离的是MED分类器,但是MED分类器没有排除距离之间的相关性和特征的方差的不同,会造成判别错误。 特征白化的目的是去除数据的冗余信息,可以通过特征白化来去除特征相关性,有两个步骤:解耦、白化。特征白化之后的欧式距离变成了马氏距离,用马氏距离作为距离衡量的是MICD分类器。但是MICD分类器的缺点是会选择方差较大的类。也还是会产生判别错误。



MAP分类器,即最大后验概率(Maximum posterior probability)分类器,基于贝叶斯规则,利用类的先验概率和观测似然概率,计算模式x属于类C的后验概率,进而进行分类判别。
其后验概率公式为:

其二分类决策边界为:
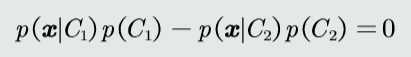
在单维空间中通常有两条决策边界,高维空间则是复杂的非线性边界。
概率误差为未选择的类的后验概率
平均概率误差:

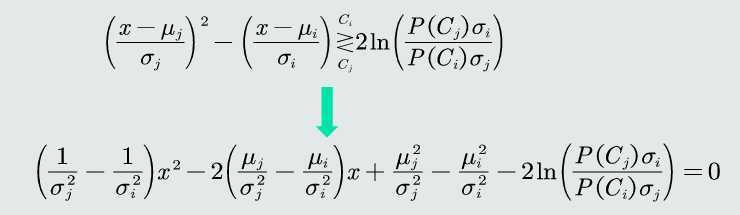



在MAP分类器基础上,加入决策风险因素,成为贝叶斯分类器
决策损失

决策目标


先验概率估计


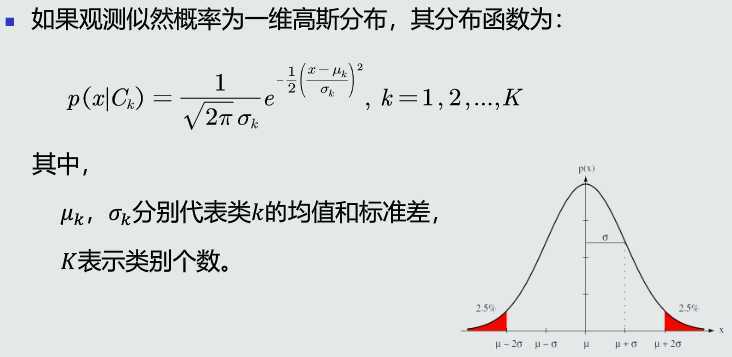
观测概率估计:高斯分布


均值估计

协方差估计



贝叶斯估计具备不断学习的能力
目的:估计观测似然概率。
给定量:观测似然分布的形式、参数的先验概率、训练样本。
贝叶斯估计的步骤:
1.估计参数的后验概率:
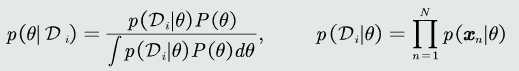
2.估计观测似然关于\(\theta\)的边缘概率:
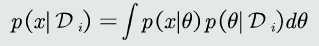

优缺点
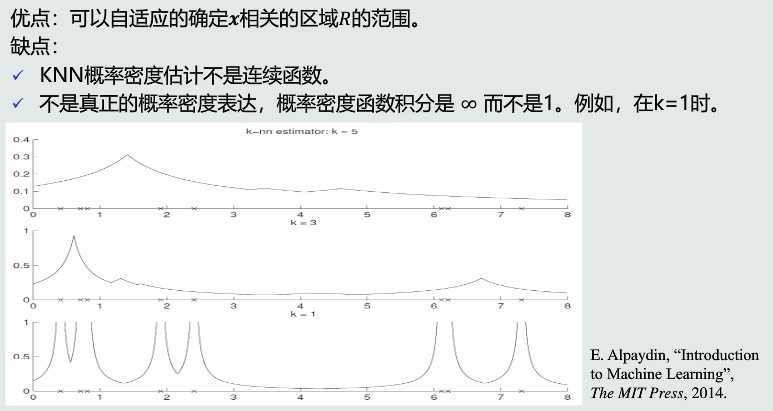
原理


优缺点

KNN估计:以待估计的任意一个模式为中心,搜寻第K个邻近点,以此来确定区域,易被噪声污染。
直方图估计:手动将特征空间划分为若干个区域,待估计模式只能分配到对应的固定区域,缺乏自适应能力。
原理



优缺点

印象最深刻的应该就是贝叶斯估计方法的学习,在参数估计上经典学派运用的是矩法和极大似然估计,贝叶斯学派则用的是Bayes估计。贝叶斯除了运用经典学派的总体信息和样本信息外,海涌到了先验信息,其中的两个基本概念是先验分布和后验分布。完成贝叶斯估计后进一步学习了贝叶斯决策问题,即把损失函数加入到贝叶斯推断中形成,根据决策者的分析和偏好可以用不同形式的损失函数。损失函数也同样是贝叶斯估计中的一种重要信息。
贝叶斯估计还具备不断学习的能力,它允许最初的、基于少量训练样本的、不太准的估计。随着训练样本的不断增加,可以串行的不断修正参数的估计值,从而达到该参数的期望真值。
定义
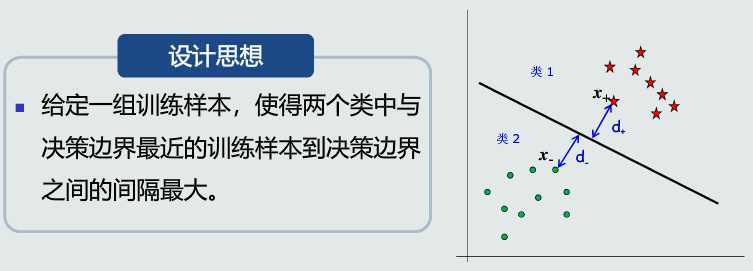
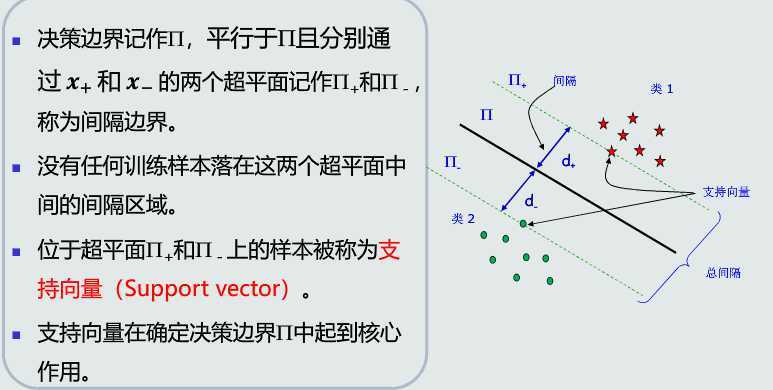
优势
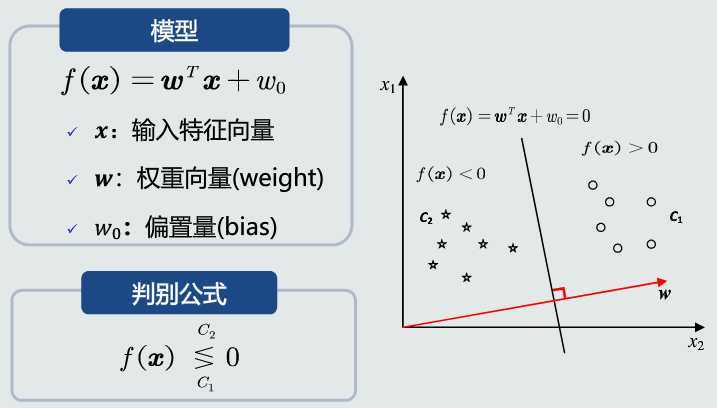
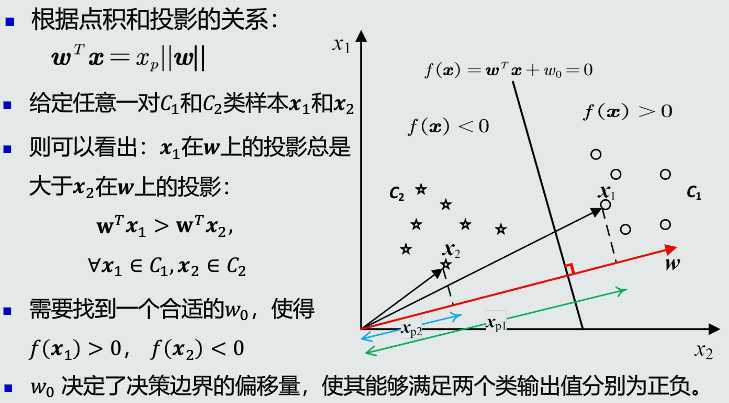
数学表达
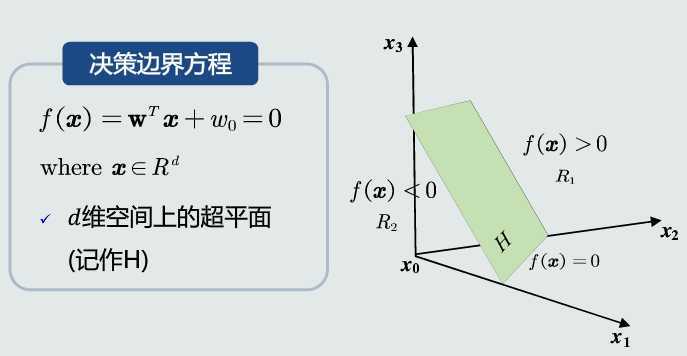
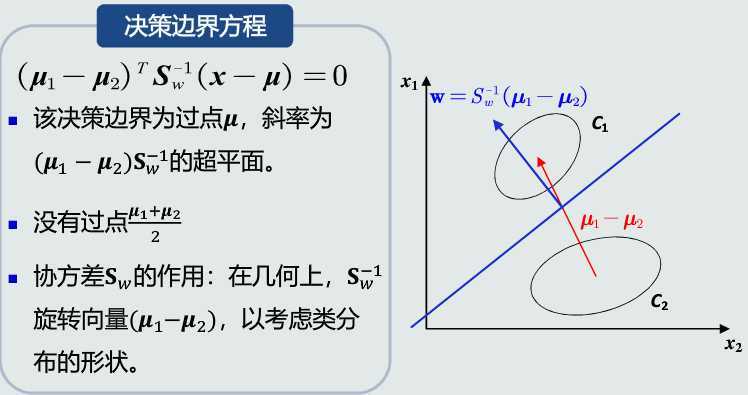
决策边界
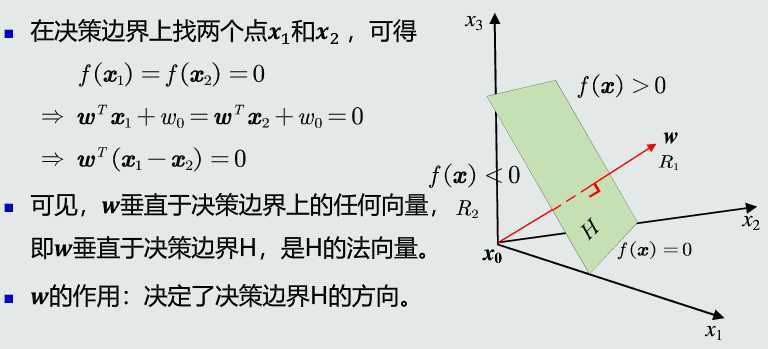
w的方向
\(w_0\)的作用







w最优解

\(w_0\)的解

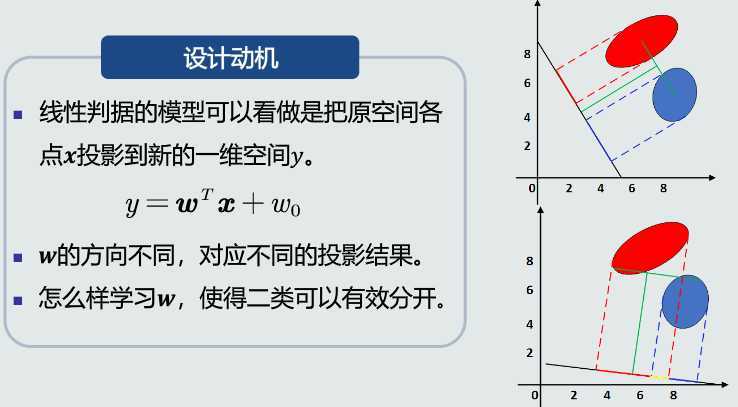
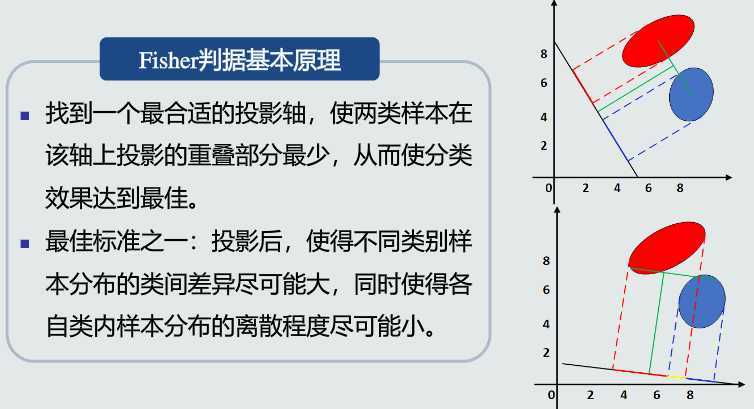
Fisher线性判据
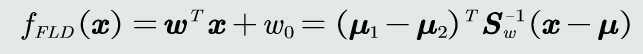




拉格朗日乘数法(以数学家约瑟夫·路易斯·拉格朗日命名)是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。
这种方法将一个有n 个变量与k个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束。
这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方程的梯度(gradient)的线性组合里每个向量的系数。此方法的证明牵涉到偏微分,全微分或链法,从而找到能让设出的隐函数的微分为零的未知数的值。
设给定二元函数z=?(x,y)和附加条件φ(x,y)=0,为寻找z=?(x,y)在附加条件下的极值点,先做拉格朗日函数 ,其中λ为参数。
令F(x,y,λ)对x和y和λ的一阶偏导数等于零,即
F‘x=?‘x(x,y)+λφ‘x(x,y)=0
F‘y=?‘y(x,y)+λφ‘y(x,y)=0
F‘λ=φ(x,y)=0
由上述方程组解出x,y及λ,如此求得的(x,y),就是函数z=?(x,y)在附加条件φ(x,y)=0下的可能极值点。
若这样的点只有一个,由实际问题可直接确定此即所求的点。




学习了线性判据方法的基本概念,并行及串行感知机算法,Fisher线性判据等,尤其对拉格朗日乘数法有了进一步的了解。
线性判据顾名思义,如果判别模型f(x)是线性函数,则称为线性判据,既可以用于两类分类,也可以用于多类分类,多类分类中要求相邻两类之间的决策边界也是线性的即可。而拉格朗日乘数法则是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。
这种方法将一个有n 个变量与k个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束,对问题的求解有很大的帮助。
原文:https://www.cnblogs.com/azeLibertas/p/12831626.html