题目: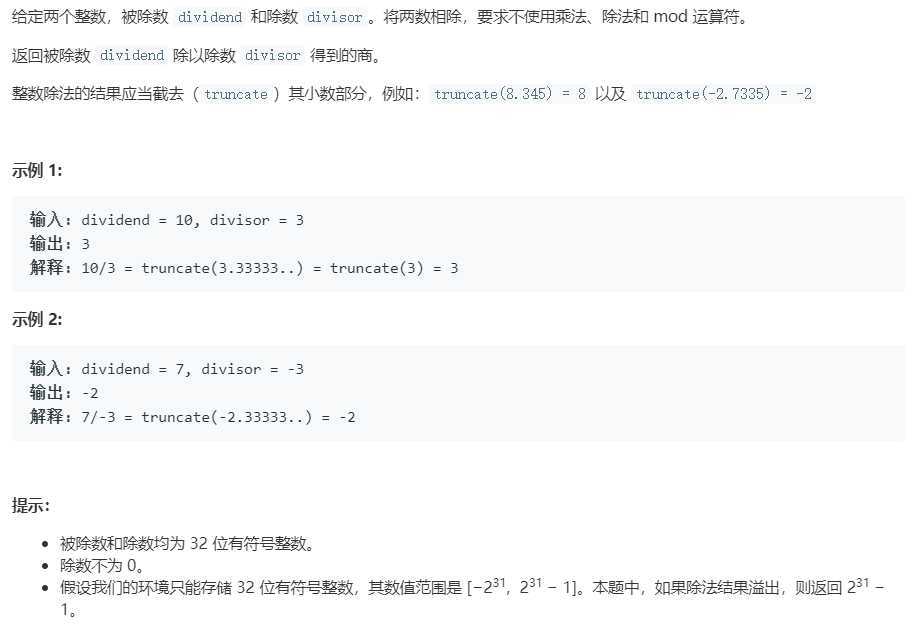
解答:
下面的方法基于这样一个事实:任何一个整数都可以表示成一个多项式的形式,例如,5 = 2^2 + 2^0,78=2^5 + 2^3 + 2^2 + 2^1等等,任何数字都可以表示上述形式。
我们使除数divisor乘以2(diveisor<<1),直到它达到或大于被除数的一半(如果我们再乘以2,它将要大于被除数dividend,让被除数让被除数dividend减去该值,假设该值被表示为divisor * 2^k,那么2^k需要加到最后的商的结果中(我们以多项式的形式表示商),一直这样处理,直到被被除数变为0。
需要注意的是:
(1)符号,总是检查除数和被除数的符号,但是上面的方法只能应用于两个正正整数,因此,必须将负数转换为正数,并且记录符号;
(2)溢出问题,注意比如INT_MAX、INT_MIN;
1 class Solution { 2 public: 3 int divide(int dividend, int divisor) 4 { 5 int sign; 6 if( (dividend >= 0 && divisor > 0) || (dividend <= 0 && divisor < 0) ) 7 { 8 sign = 0; 9 } 10 else 11 { 12 sign = 1; 13 } 14 15 long a = abs(dividend); 16 long cmp = abs(divisor); 17 18 long res = 0; 19 long partial_sum = 1; 20 21 int abs_divisor = cmp; 22 23 24 if(a < cmp) 25 { 26 return 0; 27 } 28 29 while((cmp << 1) < a) 30 { 31 cmp = cmp << 1; 32 partial_sum = partial_sum << 1; 33 } 34 35 while(a >= abs_divisor) 36 { 37 a -= cmp; 38 res += partial_sum; 39 //cout << "a: " << a << " cmp: " << cmp << " partial_sum: " << partial_sum << endl; 40 while(cmp > a) 41 { 42 cmp = cmp >> 1; 43 partial_sum = partial_sum >> 1; 44 } 45 } 46 if(sign == 1) 47 { 48 if(-res < INT_MIN) 49 { 50 return INT_MAX; 51 } 52 else 53 { 54 return -res; 55 } 56 } 57 else 58 { 59 if(res > INT_MAX) 60 { 61 return INT_MAX; 62 } 63 else 64 { 65 return res; 66 } 67 } 68 } 69 };
原文:https://www.cnblogs.com/ocpc/p/12829960.html