题目:
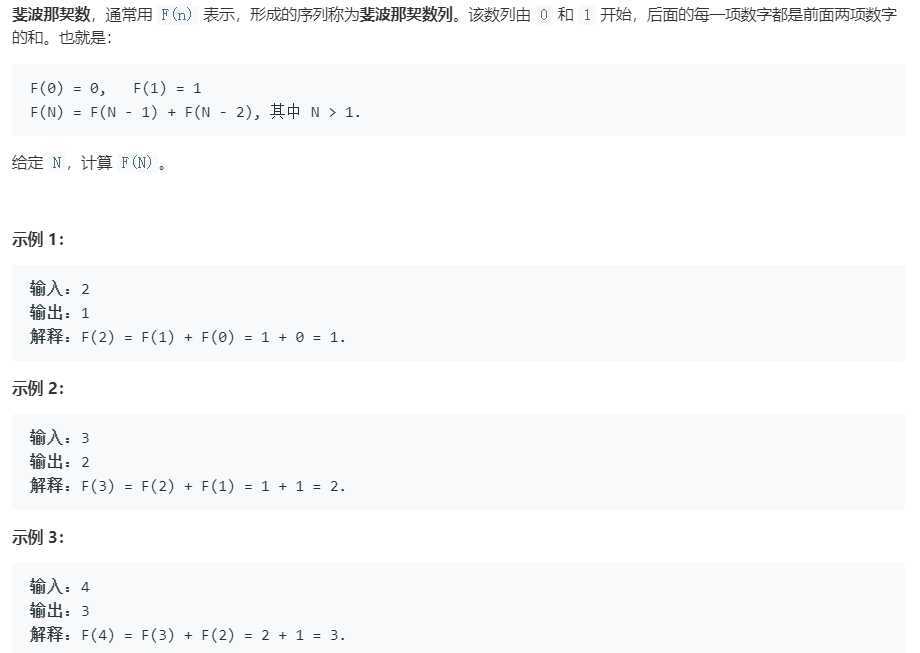
解答:
方法一:递归
算法:
(1)检查整数N,如果N小于等于1,则返回N;
(2)否则,通过递归关系:F(n) = F(n-1) + F(n-2);
(3)直到所有计算返回结果得到答案;
1 public class Solution { 2 public int fib(int N) { 3 if (N <= 1) { 4 return N; 5 } 6 return fib(N-1) + fib(N-2); 7 } 8 } 9 func fib(N int) int { 10 if N <= 1 { 11 return N 12 } 13 return fib(N-1) + fib(N-2) 14 }
方法二:记忆化自底向上的方法
自底向上通过迭代计算斐波那契数的子问题并存储已计算的值,通过已计算的值进行计算。减少递归带来的重复计算。
算法:
(1)如果N小于等于1,则返回N;
(2)迭代N,将计算出的答案存在在数组中;
(3)使用数组前面的两个斐波那契数计算当前的斐波那契数;
(4)直到我们计算到N,则返回结果。
1 class Solution { 2 public: 3 int fib(int N) 4 { 5 int i; 6 int dp[N+1]; 7 8 if(N==0) 9 { 10 return 0; 11 } 12 if(N==1) 13 { 14 return 1; 15 } 16 dp[0]=0; 17 dp[1]=1; 18 for(i=2;i<=N;i++) 19 { 20 dp[i]=dp[i-1]+dp[i-2]; 21 } 22 return dp[N]; 23 24 } 25 };
原文:https://www.cnblogs.com/ocpc/p/12827353.html